백트래킹이란?
백트래킹은 가능한 모든 경우의 수를 따라 들어가면서 탐색하는 알고리즘이다.
답이 될 수 없는 경우 더 이상 탐색하지 않고 뒤로 돌아간다.
주로 재귀 함수를 사용해 구현한다.
시간 복잡도는 O(N!)으로 매우 큰 편이다. 그렇기 때문에 백트래킹 관련 문제에서는 N이 작게 주어진다.
백트래킹 구현에서 가장 중요한 점은 방문 상태 변화 & 상태 원상 복구 두 가지다. 로직을 작성할 때 항상 염두에 두자.
백트래킹과 순열, 조합
순열과 조합을 구할 때, 가능한 모든 경우의 수에 대해 검사하기 때문에 백트래킹을 사용할 수 있다.
아래에서 설명하는 순열과 조합은 오름차순으로 정렬된 집합을 기준으로 한다.
아래 코드에서 공통적으로 나오는 변수들은 다음을 나타낸다.
- isUsed[i]: i번째 수가 사용되었는 지 여부를 저장
- arr[i]: 입력받은 수를 저장
- selected[k]: k번째 자리에 들어갈 수
- arrSize: 전체 집합의 크기
- sel: 집합에서 고를 원소의 개수
- cnt: 경우의 수
순열

#include <bits/stdc++.h>
using namespace std;
// 입력받은 수와 그 수의 사용 여부
bool isUsed[10];
int arr[10];
int selected[10]; // 선택된 수
int arrSize; // 배열 크기는 1 ~ 9
int sel; // 고를 원소의 개수
int cnt = 0; // 경우의 수
// 순열
// 순서 O
// 중복 X
// 순열에서 k번째 자리의 수를 결정
void func(int k)
{
if (k == sel) // 모든 수를 골랐다면 그 수열을 출력
{
for (int i = 0; i < sel; i++)
{
cout << selected[i] << " ";
}
cout << endl;
cnt++;
return;
}
for (int i = 1; i <= arrSize; i++)
{
if (!isUsed[i]) // 만약 i번째 수가 사용중이지 않으면
{
isUsed[i] = true; // 상태 변화
selected[k] = arr[i]; // k번째 자리의 수를 입력받은 수 중 i번째 수로 결정
func(k + 1); // 다음 자리 결정
isUsed[i] = false; // 상태 복구
}
}
}
int main()
{
cin >> arrSize >> sel;
for (int i = 1; i <= arrSize; i++)
{
int input;
cin >> input;
arr[i] = input;
}
func(0);
cout << cnt << endl;
}func는 순열에서 k번째에 올 값을 결정하는 함수다. 코드를 자세히 살펴보자.
if (k == sel) // 모든 수를 골랐다면 그 수열을 출력
{
for (int i = 0; i < sel; i++)
{
cout << selected[i] << " ";
}
cout << endl;
cnt++;
return;
}k는 순열에서의 각 자리에 올 수를 결정할 때마다 재귀 호출에 의해 1씩 증가한다. 만약 k가 고르는 원소의 개수인 sel과 같아진다면 모든 자리를 채운 것이므로 결과를 출력하고 경우의 수를 1 증가시킨다.
for (int i = 1; i <= arrSize; i++)
{
if (!isUsed[i]) // 만약 i번째 수가 사용중이지 않으면
{
isUsed[i] = true; // 상태 변화
selected[k] = arr[i]; // k번째 자리의 수를 입력받은 수 중 i번째 수로 결정
func(k + 1); // 다음 자리 결정
isUsed[i] = false; // 상태 복구
}
}arr에 담긴 입력받은 모든 수에 대해 검사를 한다. 만약 i번째 수가 사용되지 않았다면, 사용 상태로 변경한 뒤, k번째 자리를 해당 값으로 결정한다. 그런 뒤에 다음 자리를 결정하기 위해 k+1를 증가시켜 func 함수를 재귀호출한다. 안쪽에서 모든 처리가 끝나면 사용 상태를 다시 원래대로 되돌린다.
해당 구조를 쉽게 나타내면 다음과 같다.

1, 2, 3, 4, 5 다섯 개의 수 중에서 3개를 뽑는 순열을 구한다고 하자. 그럼 위의 사진과 같은 구조가 될 것이다. selected의 첫 번째 자리에 올 수 있는 수는 입력받은 모든 수 중 아무거나 올 수 있다. 먼저 첫 번째 자리에 1을 놓자.

1이 사용중이지 않으므로, 사용 여부를 T로 바꾸고 첫 번째 자리에 1을 놓는다.
그런 다음 그 다음 자리에 올 수 있는 수를 찾는다. 그 다음 수인 2가 사용중이지 않으므로 두 번째 자리에 2를 놓는다.

이전과 동일하게 사용 여부를 T로 바꾸고 2를 놓는다. 그 다음 자리도 비었으므로 동일하게 처리한다.
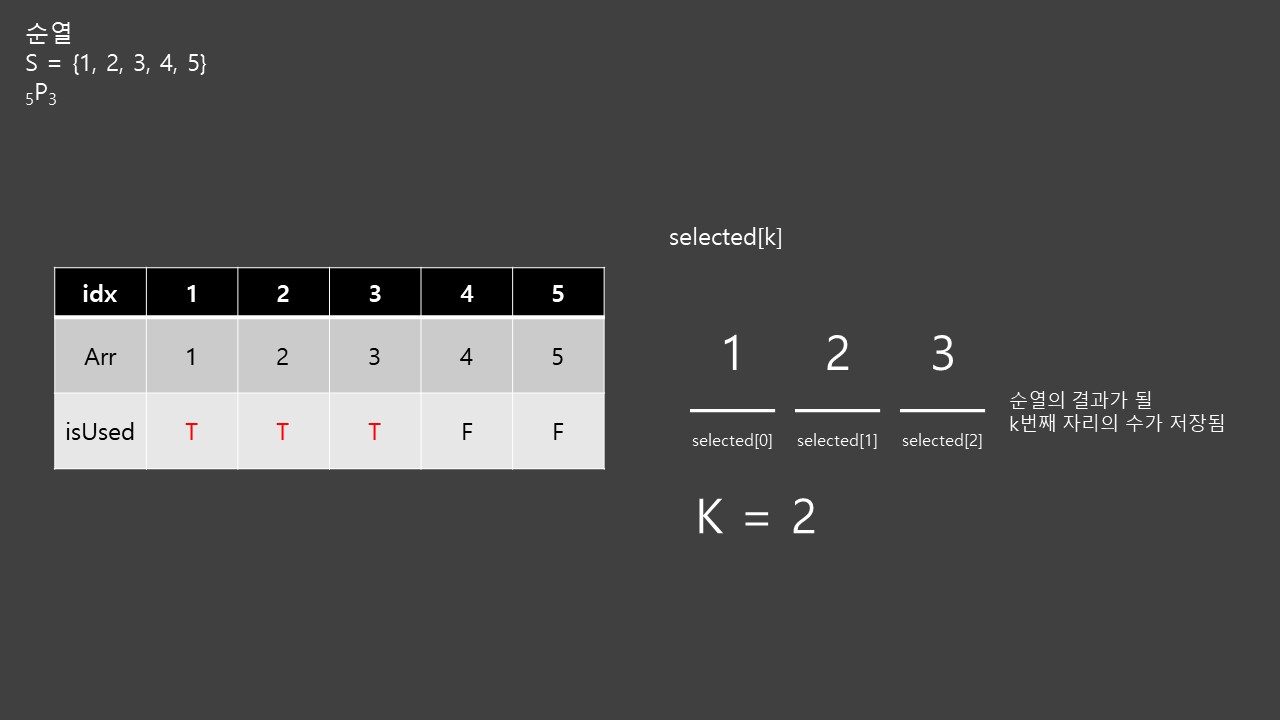
이 상태에서 재귀 호출을 하면 K=3이 되므로 결과를 출력하고 다시 돌아와서 isUsed[3]을 F로 바꾼다. 그런 다음 K=2일때의 재귀 함수에 있는 for문에 의해 다음 수인 4를 집어넣게 된다.
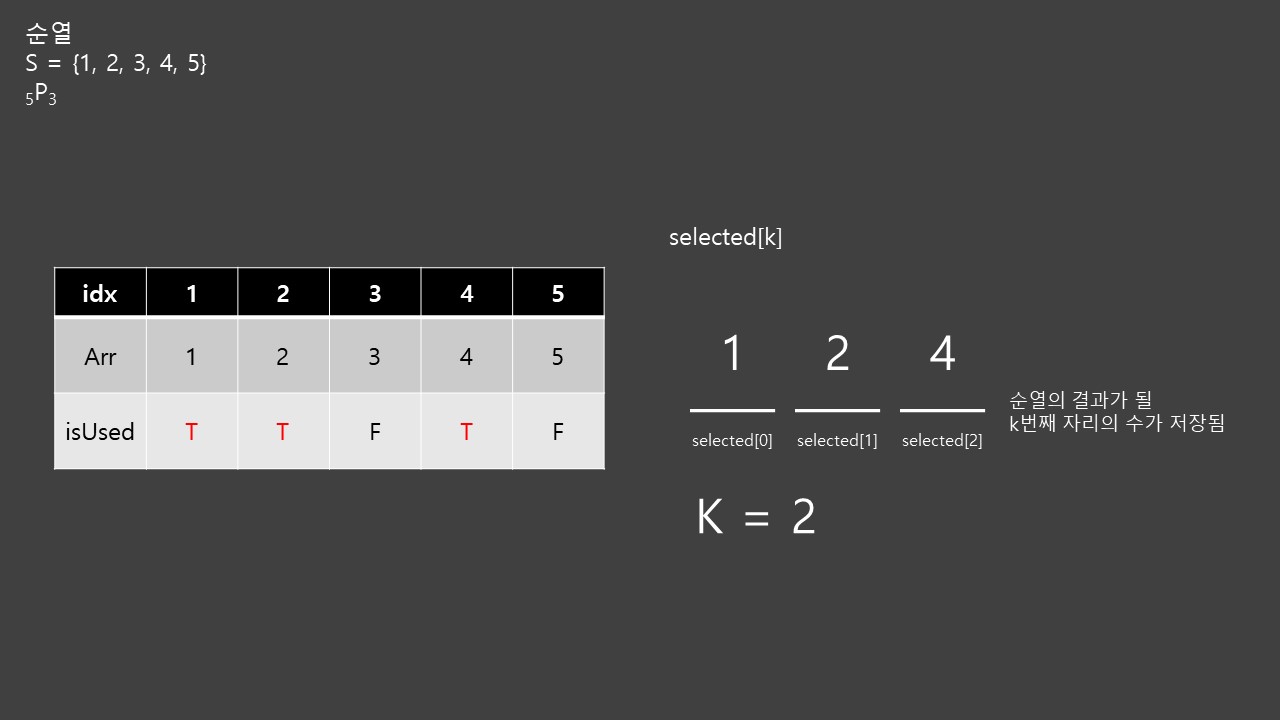
이렇게 반복하면 순열의 모든 결과를 구할 수 있다.
조합

#include <bits/stdc++.h>
using namespace std;
int arr[10]; // 입력받은 수
int selected[10]; // 선택된 수
int arrSize; // 배열 크기는 1 ~ 9
int sel; // 고를 원소의 개수
int cnt = 0; // 경우의 수
// 조합
// 순서 X
// 중복 X
// 조합에서 k번째 자리의 수를 결정
// 조합은 이전에 나온 수가 나오면 안되므로 idx로 뽑을 수 있는 수의 범위를 결정
void func(int k, int idx)
{
if (k == sel) // 모든 수를 골랐다면 그 수열을 출력
{
for (int i = 0; i < sel; i++)
{
cout << selected[i] << " ";
}
cout << endl;
cnt++;
return;
}
for (int i = idx; i <= arrSize; i++)
{
selected[k] = arr[i]; // k번째 자리의 수를 입력받은 수 중 i번째 수로 결정
func(k + 1, i + 1); // 다음 자리 결정. 다음 자리에 올 수 있는 수의 범위의 시작을 현재 뽑은 수의 다음 수부터로 결정
}
}
int main()
{
cin >> arrSize >> sel;
for (int i = 1; i <= arrSize; i++)
{
int input;
cin >> input;
arr[i] = input;
}
func(0, 1);
cout << cnt << endl;
}조합은 쉽게 말하자면 한쪽 방향으로만 선택하면 된다. 즉, 현재 자리에 올 수 있는 수는 이전 자리에 있는 수보다 큰 수가 오면 된다. 조건 검사 부분은 순열과 같으므로 바뀐 부분만 살펴보자.
void func(int k, int idx)for (int i = idx; i <= arrSize; i++)
{
selected[k] = arr[i]; // k번째 자리의 수를 입력받은 수 중 i번째 수로 결정
func(k + 1, i + 1); // 다음 자리 결정. 다음 자리에 올 수 있는 수의 범위의 시작을 현재 뽑은 수의 다음 수부터로 결정
}매 루프마다 1부터 시작해 모든 수의 사용 여부를 검사하는 순열과 달리, 조합은 한쪽 방향으로만 선택되어야 하기 때문에 매 루프의 시작 지점을 지정해 범위를 제한한다. 그리고 한쪽 방향으로만 선택된다는 성질때문에 집합에 중복되는 수가 없다면 사용 여부를 검사할 필요가 없다.
코드만 보면 이해하기 어려울 수 있으니 그림으로 살펴보자.

첫 번째 자리에 올 수 있는 수를 정한다. 먼저 1를 집어넣는다.
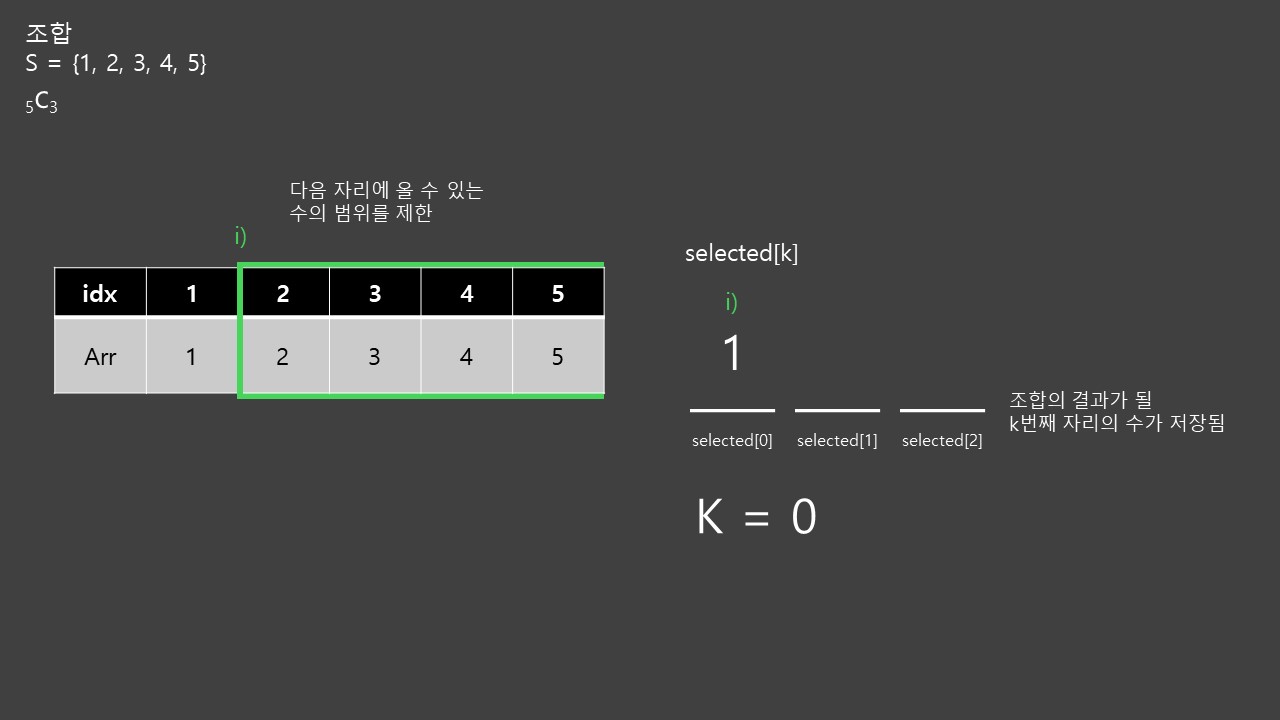
한쪽 방향으로만 선택해야 하기 때문에 다음 단계의 재귀 함수의 idx값에 i + 1 = 2를 인수로 넘긴다. 그러면 다음 단계의 for문은 idx부터 시작하므로 새로운 범위가 만들어진다. 두 번째 자리에 2가 들어가는 경우부터 조금 건너 뛰어서 다음 자리에 3이 오는 경우를 살펴보자.

인수로 i + 1 = 4가 전달된다. 그러면 이전과 같이 다음 자리에 올 수 있는 수에 대해 새로운 범위가 생긴다. 세 번째 자리에 4가 들어가는 경우를 건너 뛰고, 5가 들어가는 경우를 살펴보자.

이 상태에서 다음 자리를 채우려고 시도하면 K=3이 되어 결과를 출력하고 다시 돌아온다.
이 과정을 반복하면 조합의 모든 결과를 구할 수 있다.
중복순열
#include <bits/stdc++.h>
using namespace std;
int arr[10]; // 입력받은 수
int selected[10]; // 선택된 수
int arrSize; // 배열 크기는 1 ~ 9
int sel; // 고를 원소의 개수
int cnt = 0; // 경우의 수
// 중복 순열
// 순서 O
// 중복 O -> isUsed 배열이 필요 없음
// 순열에서 k번째 자리의 수를 결정
void func(int k)
{
if (k == sel) // 모든 수를 골랐다면 그 수열을 출력
{
for (int i = 0; i < sel; i++)
{
cout << selected[i] << " ";
}
cout << endl;
cnt++;
return;
}
for (int i = 1; i <= arrSize; i++)
{
selected[k] = arr[i]; // k번째 자리의 수를 입력받은 수 중 i번째 수로 결정
func(k + 1); // 다음 자리 결정
}
}
int main()
{
cin >> arrSize >> sel;
for (int i = 1; i <= arrSize; i++)
{
int input;
cin >> input;
arr[i] = input;
}
func(0);
cout << cnt << endl;
}중복순열은 순열에서 사용 여부를 검사하는 isUsed 배열에 대한 처리만 빼면 된다.
중복조합
#include <bits/stdc++.h>
using namespace std;
int arr[10]; // 입력받은 수
int selected[10]; // 선택된 수
int arrSize; // 배열 크기는 1 ~ 9
int sel; // 고를 원소의 개수
int cnt = 0; // 경우의 수
// 중복조합
// 순서 X
// 중복 O
// 조합에서 k번째 자리의 수를 결정
// 조합은 이전에 나온 수가 나오면 안되므로 idx로 뽑을 수 있는 수의 범위를 결정
void func(int k, int idx)
{
if (k == sel) // 모든 수를 골랐다면 그 수열을 출력
{
for (int i = 0; i < sel; i++)
{
cout << selected[i] << " ";
}
cout << endl;
cnt++;
return;
}
for (int i = idx; i <= arrSize; i++)
{
selected[k] = arr[i]; // k번째 자리의 수를 입력받은 수 중 i번째 수로 결정
func(k + 1, i); // i + 1이 아니라 i를 넘겨 현재 뽑은 수를 다음 단계에서 다시 뽑을 수 있도록 함
}
}
int main()
{
cin >> arrSize >> sel;
for (int i = 1; i <= arrSize; i++)
{
int input;
cin >> input;
arr[i] = input;
}
func(0, 1);
cout << cnt << endl;
}중복조합은 이전 자리에서 나온 수를 현재 자리에 다시 사용할 수 있다. 그렇기 때문에 범위를 제한하는 func 함수의 idx에 인수로 자기 자신을 가리키는 인덱스인 i를 넘겨 다시 사용할 수 있게 하면 된다.
'Programming > Algorithm & Data Structure' 카테고리의 다른 글
| [Algorithm] 선택 정렬 (Selection Sort) (0) | 2025.01.09 |
|---|---|
| [Algorithm, C++] next_permutation, prev_permutation과 순열, 조합 (0) | 2024.09.10 |
| [Algorithm] DFS (다차원 배열) (0) | 2024.08.11 |
| [Algorithm] BFS (다차원 배열) (0) | 2024.08.10 |
| [Algorithm] 델타값을 이용한 상하좌우 탐색 (0) | 2024.08.05 |
