[Data Structure] 트리, 이진 트리

트리 (Tree)

https://en.wikipedia.org/wiki/Tree_%28abstract_data_type%29

트리의 정의

트리는 한 개 이상의 노드로 이루어진 유한 집합으로서

• 노드 중에는 루트(root)라고 하는 노드가 하나 있고
• 나머지 노드들은 n개의 분리 집합 T1, T2, ..., Tn으로 분할 될 수 있다. 이때, 분리 집합 T1, T2, ..., Tn은 각각 하나의 트리이며 루트의 서브트리라고 한다.

트리의 구조 및 용어

트리 용어

• 차수(degree): 어떤 노드의 자식 개수
• 리프(leaf) 또는 단말(terminal) 노드: 차수가 0인 노드
• 자식(children): 어떤 노드 X의 서브트리의 루트들
• 부모(parent): 어떤 노드 X
• 형제(sibling): 부모가 같은 자식들
• 트리의 차수(degree of tree): 그 트리에 있는 노드의 최대 차수
• 조상(ancestor): 루트에서 그 노드까지의 경로 상에 있는 모든 노드
• 레벨(level): 루트의 레벨을 1 또는 0으로 정의 후, 자식으로 내려갈 수록 1씩 증가
• 높이(height) 또는 깊이(depth): 그 트리에 속한 노드의 최대 레벨

트리의 표현

중첩된 괄호

( A(B(E(K,L),F),C(G),D(H(M)),I,J))) 와 같이 루트 노드가 제일 먼저 나오고 서브트리들의 리스트가 다음에 나온다.

연결 리스트 표현

구조체, 클래스 등을 사용해 데이터와 자식들에 대한 포인터를 각 노드에 담음. 하지만 노드 크기가 고정되는 것이 데이터 표현에 용이하므로 대부분 일정 크기의 노드들만 사용한다.

왼쪽 자식 - 오른쪽 형제 노드 구조

데이터
자식 노드	형제 노드

와 같은 형태로 한 개의 포인터에는 가장 왼쪽 자식, 오른쪽 포인터에는 자신의 바로 오른쪽에 있는 형제 노드를 가리키게 한다.

 

트리는 대부분 이진 트리에 대해서만 다루므로 가볍게 보고 넘어가자.

이진 트리 (Binary Tree)

https://en.wikipedia.org/wiki/Binary_tree

이진 트리의 정의

공백이거나 루트와 왼쪽 서브트리, 오른쪽 서브트리라고 하는 두 개의 분리된 이진 트리로 구성된 노드의 유한 집합이다.

 

일반적인 트리에서는 서브트리의 순서가 관계 없지만, 이진 트리에서는 왼쪽 서브트리와 오른쪽 서브트리를 구별한다.

이진 트리의 종류

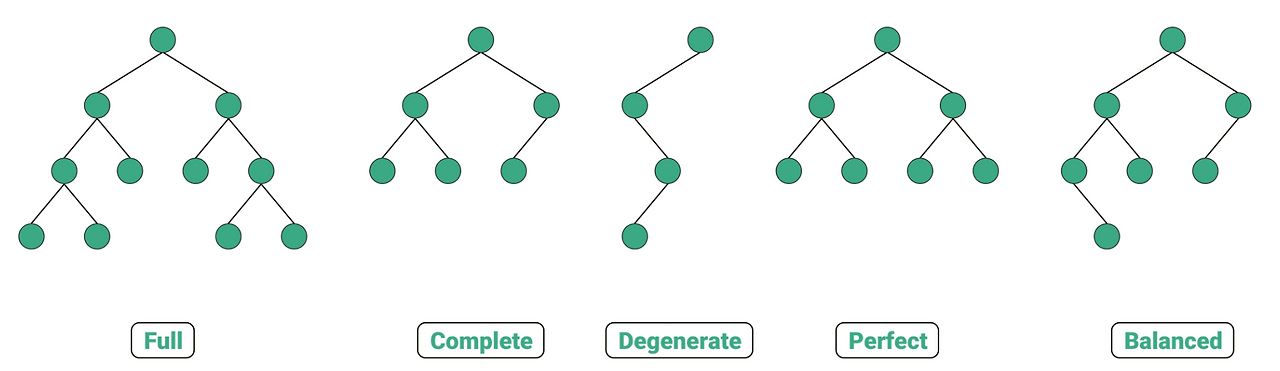
• 전 이진 트리 (Full Binary Tree): 모든 노드가 0개 또는 2개의 자식을 갖는 트리
• 포화 이진 트리 (Perfect Binary Tree): 모든 레벨이 노드로 가득 차있는 트리
• 완전 이진 트리 (Complete Binary Tree): 마지막 레벨을 제외하고 이전 레벨까지는 모두 채워져 있고, 노드는 왼쪽에서 오른쪽으로 채워진 트리
• 편향 이진 트리 (Skewed Binary Tree): 한 쪽 방향으로만 계속 연결된 트리

이진 트리의 성질

이진 트리 최대 노드 수

• 이진 트리의 레벨 i의 최대 노드 수는 2^(i-1)
• 깊이가 k인 이진 트리의 최대 노드 수는 2^k - 1

이진 트리의 높이

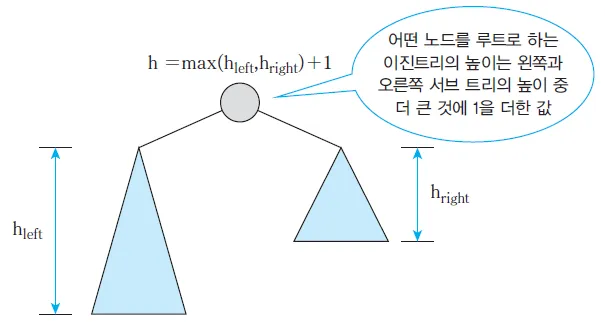
어떤 노드를 루트로 하는 이진 트리의 높이는 왼쪽, 오른쪽 서브트리의 높이 중 더 큰 것에 1을 더한 값이다.

int GetHeight(Node root)
{
	if (root == nullptr)
    	return 0;
        
       hLeft = GetHeight(root.left);
       hRight = GetHeight(root.right);
       return max(hLeft, hRight) + 1;
}

 

 

이진 트리의 표현

배열 표현

https://blog.skku-comit.dev/cc-binary-tree-1

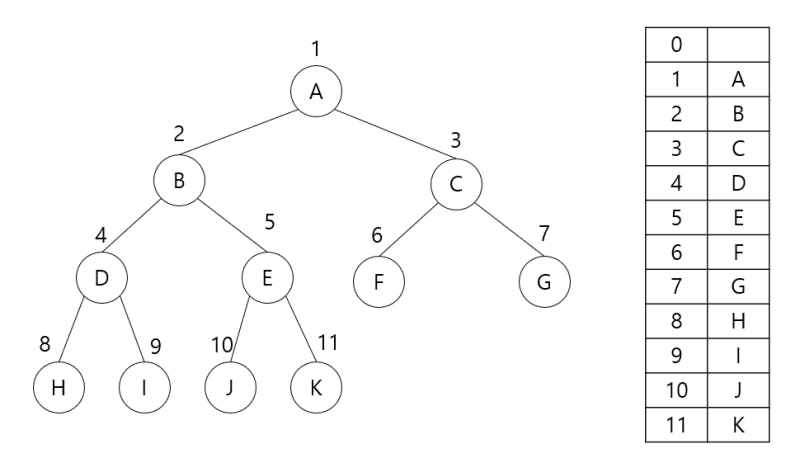
n개의 노드가 있을 때, 노드에 1부터 n까지 번호를 할당하면 1차원 배열에 저장할 수 있다.

이진 트리를 배열로 표현했을 때, 루트 노드가 1번부터 시작하고 왼쪽에서 오른쪽으로 갈 수록 1씩 증가한다고 하면 n번째 노드의

• 부모 노드의 인덱스: n/2
• 왼쪽 자식 노드의 인덱스: 2*n
• 오른쪽 자식 노드의 인덱스: 2*n + 1

완전 이진 트리의 경우에는 낭비되는 공간이 없어 이상적이지만 편향 트리의 경우에는 낭비가 매우 심하다.

연결 표현

연결 표현(linked representation)을 사용하면 공간의 낭비를 줄일 수 있다.

http://www.btechsmartclass.com/data_structures/binary-tree-representations.html

http://www.btechsmartclass.com/data_structures/binary-tree-representations.html

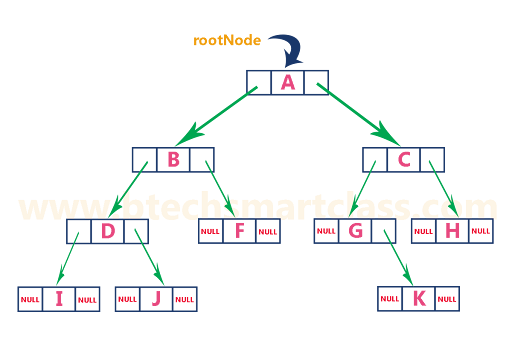
template <typename T>
class TreeNode
{
    public:
        TreeNode(T data)
        {
            this->data = data;
        }

    T data;
    TreeNode<T>* left;
    TreeNode<T>* right;
};

이러한 노드 구조에서는 부모를 알기 어렵다는 단점이 있지만, 노드에 parent 필드를 추가하면 된다.

이진 트리 구현 코드

template <typename T>
class BinaryTree
{
public:
    // 빈 이진 트리 생성
    BinaryTree() {}

    // 왼쪽 서브트리, 오른쪽 서브트리, 값을 갖는
    // 이진트리 생성
    BinaryTree(BinaryTree<T>* leftSubTree, T data, BinaryTree<T>* rightSubTree)
    {
        TreeNode<T>* newNode = new TreeNode(data);
        newNode->left = leftSubTree->GetRootNode();
        newNode->right = rightSubTree->GetRootNode();
        root = newNode;
    }

    // 이진 트리 공백 여부
    bool IsEmpty()
    {
        if (root)
            return false;
        else
            return true;
    }
    
    TreeNode<T>* GetRootNode()
    {
        if (IsEmpty())
        {
            std::cout << "Binary tree is empty\n";
            return nullptr;
        }
        else
            return this->root;
    }

    TreeNode<T>* GetLeftSubtree()
    {
        if (IsEmpty())
        {
            std::cout << "Binary tree is empty\n";
            return nullptr;
        }
        else
            return this->root.left;
    }

    TreeNode<T>* GetRightSubtree()
    {
        if (IsEmpty())
        {
            std::cout << "Binary tree is empty\n";
            return nullptr;
        }
        else
            return this->root.right;
    }

    T RootData()
    {
        if (IsEmpty())
        {
            std::cout << "Binary tree is empty\n";
            return NULL;
        }
        else
            return this->root.data;
    }
    
private:
    TreeNode<T>* root = nullptr; // root node
};