728x90
힙 트리 (Heap Tree)
- 우선순위 큐를 위해 최대 또는 최소값을 빠르게 검색하는 자료구조
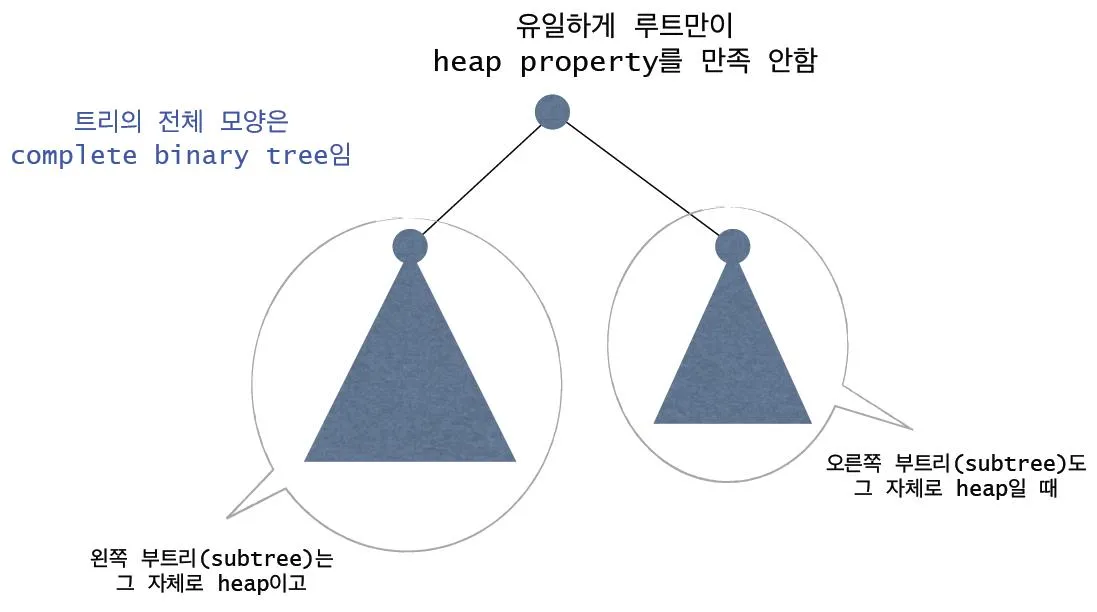
- 완전 이진 트리의 일종
- 아래에서 나올 Heap Property 중 하나를 만족해야 함
- 반정렬(느슨한 정렬) 상태를 유지함
- Max Heap Property 기준, 부모보다 작기만 하면 되므로 부모-자식 관계가 아닌 다른 노드들끼리는 정렬 관계 상관 X
- 서브 트리가 힙 트리면 서브 트리의 서브 트리도 힙 트리

힙 트리 판단하기
힙 트리인지 판단하기 위해선 다음 두 가지를 확인하면 된다.
- 완전 이진 트리인가?
- Heap Property를 만족하는가?

Heap Property
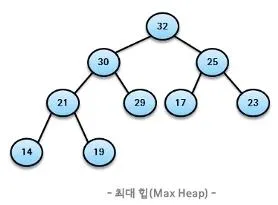
Max-heap Property
- 부모가 자식보다 항상 크거나 같은 성질
- 루트 노드가 항상 최댓값을 가짐
- 서브 트리의 루트 노드는 해당 서브 트리에서 최댓값을 가짐
Min-heap Property
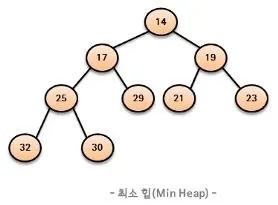
- 부모가 자식보다 항상 작거나 같은 성질
- 루트 노드가 항상 최솟값을 가짐
- 서브 트리의 루트 노드는 해당 서브 트리에서 최솟값을 가짐
Max-Heapify
Max-Heapify 개요
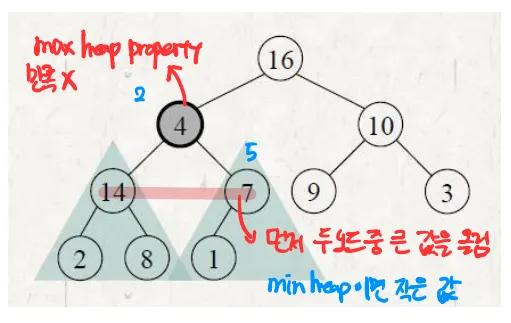
- Heapify란 Heap Property를 어기고 있을 때 바로 잡는 과정을 뜻함
- Max-Heapify는 특정 노드를 기준으로 Max-heap Property를 만족하도록 재구성하는 과정
- 시간 복잡도는 O(logn)
- 트리의 높이만큼 반복될 수 있기 때문
Max-Heapify 과정
- 만약 자식 노드가 없다면 leaf 노드이므로 종료
- 두 자식 노드의 값을 비교해 더 큰 노드의 인덱스를 구함
- 루트 노드가 더 큰 자식 노드보다 작다면 Swap
- Swap으로 이동한 서브 트리에 대해 재귀적으로 다시 반복
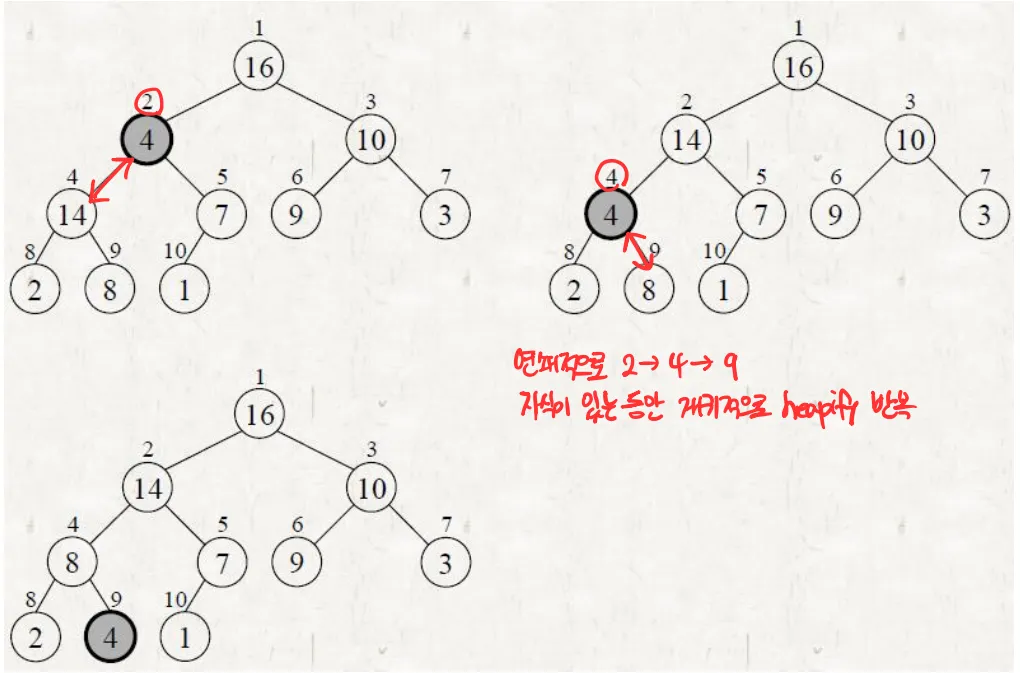
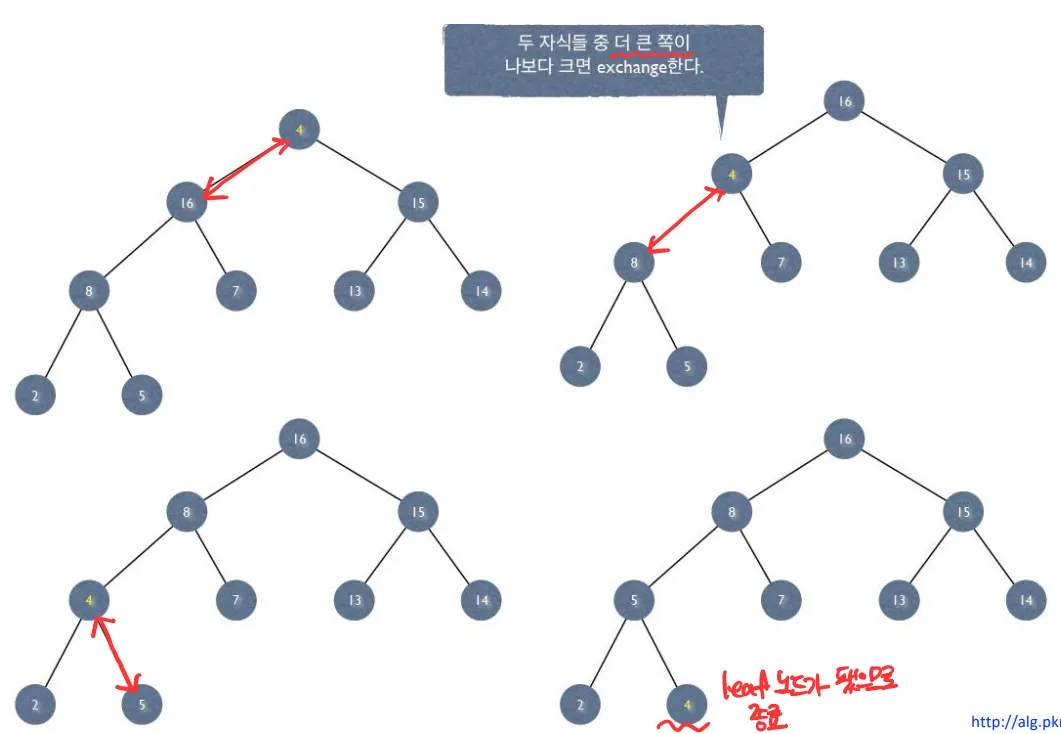
// 루트에서 시작해 리프 노드까지
void MaxHeapify(int idx)
{
int leftChildIdx = -1, rightChildIdx = -1;
// 두 자식이 범위 안에 있으면 인덱스 설정
if (2*idx <= heapSize)
leftChildIdx = 2*idx;
if (2*idx + 1 <= heapSize)
rightChildIdx = 2*idx + 1;
int compChildIdx = -1; // 비교할 자식 노드 인덱스
if (leftChildIdx == -1 && rightChildIdx == -1) // 리프 노드인 경우
return;
else if (rightChildIdx == -1) // 왼쪽 자식 노드만 있는 경우
compChildIdx = leftChildIdx;
else if (heap[leftChildIdx] > heap[rightChildIdx])
compChildIdx = leftChildIdx;
else
compChildIdx = rightChildIdx;
// 현재 노드와 비교
if (heap[idx] < heap[compChildIdx]) // 더 큰 경우 swap
{
std::swap(heap[idx], heap[compChildIdx]);
MaxHeapify(compChildIdx); // 바꾼 자리에서 다시 Max-Heapify
}
}Build Max Heap
Build Max Heap 개요
- 전체 배열을 최대 힙으로 만드는 과정
- Max-Heapify와 함께 사용되는 개념
Build Max Heap 과정
- 주어진 배열을 바닥부터 위로 올라가면서 Max-Heapify를 반복 적용해 최대 힙 구조로 만듦
- 가장 마지막 leaf 노드의 부모 노드부터 루트 노드까지 올라감
- 가장 마지막 부모 노드의 인덱스는 전체 노드 개수(배열 크기) / 2
- 시간 복잡도는 O(n)
// 마지막 부모 노드부터 루트 노드까지 올라오면서 Max-Heapify를 진행
// 마지막 부모 노드 인덱스 -> 배열 길이 / 2
void BuildMaxHeap()
{
for (int i = heapSize/2; i > 0; i--)
{
MaxHeapify(i);
}
}최대 힙 노드 Push

맨 마지막에 새로운 노드를 붙인 후, 새 노드에서 시작해 루트 쪽으로 올라가며 Max-Heapify를 해야 한다.
void Push(const T& value)
{
// 힙이 꽉 찬 경우 2배로 늘림
if (heapSize == capacity)
{
T* temp = new T[capacity*2];
memcpy(temp, heap, capacity * sizeof(T));
delete heap;
heap = temp;
capacity *= 2;
}
heap[++heapSize] = value;
BuildMaxHeap();
}최대 힙 Pop
힙이 다음과 같은 상태라고 하자.

힙의 루트 노드(최댓값)을 Pop 하려면 다음 과정이 필요하다.
- 루트 노드의 값을 뺀다.
- 힙의 맨 마지막 노드를 루트로 올린다.
- 루트부터 Max-Heapify를 한다.


void Pop()
{
T last = heap[heapSize--]; // 마지막 원소
heap[1] = last; // 루트로 올림
MaxHeapify(1);
}최소 힙, Min Heapify, Build Min Heap
최대 힙과 구현은 매우 비슷하고, 대소 비교하는 부분만 바꿔주면 된다.

최대 힙 전체 코드
#include <iostream>
template <typename T>
class MaxHeap
{
public:
MaxHeap(int capacity = 10)
{
if (capacity < 1)
{
std::cout << "Capacity must be >= 1";
return;
}
this->capacity = capacity;
heapSize = 0;
heap = new T[capacity + 1]; // 완전 이진 트리이므로 heap[0] 사용 X
}
// 루트에서 시작해 리프 노드까지
void MaxHeapify(int idx)
{
int leftChildIdx = -1, rightChildIdx = -1;
// 두 자식이 범위 안에 있으면 인덱스 설정
if (2*idx <= heapSize)
leftChildIdx = 2*idx;
if (2*idx + 1 <= heapSize)
rightChildIdx = 2*idx + 1;
int compChildIdx = -1; // 비교할 자식 노드 인덱스
if (leftChildIdx == -1 && rightChildIdx == -1) // 리프 노드인 경우
return;
else if (rightChildIdx == -1) // 왼쪽 자식 노드만 있는 경우
compChildIdx = leftChildIdx;
else if (heap[leftChildIdx] > heap[rightChildIdx])
compChildIdx = leftChildIdx;
else
compChildIdx = rightChildIdx;
// 현재 노드와 비교
if (heap[idx] < heap[compChildIdx]) // 더 큰 경우 swap
{
std::swap(heap[idx], heap[compChildIdx]);
MaxHeapify(compChildIdx); // 바꾼 자리에서 다시 Max-Heapify
}
}
// 마지막 부모 노드부터 루트 노드까지 올라오면서 Max-Heapify를 진행
// 마지막 부모 노드 인덱스 -> 배열 길이 / 2
void BuildMaxHeap()
{
for (int i = heapSize/2; i > 0; i--)
{
MaxHeapify(i);
}
}
void Push(const T& value)
{
// 힙이 꽉 찬 경우 2배로 늘림
if (heapSize == capacity)
{
T* temp = new T[capacity*2];
memcpy(temp, heap, capacity * sizeof(T));
delete heap;
heap = temp;
capacity *= 2;
}
heap[++heapSize] = value;
BuildMaxHeap();
}
void Pop()
{
T last = heap[heapSize--]; // 마지막 원소
heap[1] = last; // 루트로 올림
MaxHeapify(1);
}
T& Top()
{
return heap[1];
}
void Print()
{
for (int i = 1; i <= heapSize; i++)
{
if (i % 2 == 0)
std::cout << "\n";
std::cout << heap[i] << " ";
}
}
private:
T* heap; // 힙 배열 (양의 정수만 들어온다고 가정)
int heapSize; // 힙에 있는 원소 수
int capacity; // heap 배열 크기
};728x90
'Programming > Algorithm & Data Structure' 카테고리의 다른 글
| [Data Structure] 이진 탐색 트리 (0) | 2025.01.13 |
|---|---|
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2025.01.13 |
| [Data Structure] 이진 트리 순회 (0) | 2025.01.13 |
| [Data Structure] 트리, 이진 트리 (0) | 2025.01.12 |
| [Data Structure] 이중 연결 리스트 (0) | 2025.01.12 |
