728x90
Dynamic Set
- 검색, 삭제, 삽입 등의 연산을 지원하는 자료구조를 통틀어 Dynamic Set이라 한다.
- Dynamic Set을 구현하려면
- 배열, 연결 리스트, 해시 테이블 등 선형 구조를 이용 -> Insert, Search, Delete 중 적어도 하나는 O(n)
- 이진 탐색 트리, 레드-블랙 트리, AVL 트리 등의 트리 기반 구조 이용 -> 모두 O(logn)
이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리 개요
- 자료를 빠르게 검색하기 위한 검색 트리 중 하나
- 이진 트리의 구조를 가짐
- 각 노드에 하나의 Key만 저장
- 임의의 노드 v에 대하여
- 왼쪽 서브트리에 있는 Key들은 Key[V]보다 작거나 같다.
- 오른쪽 서브트리에 있는 Key들은 Key[V]보다 크거나 같다.
- 서브트리도 이진 검색 트리
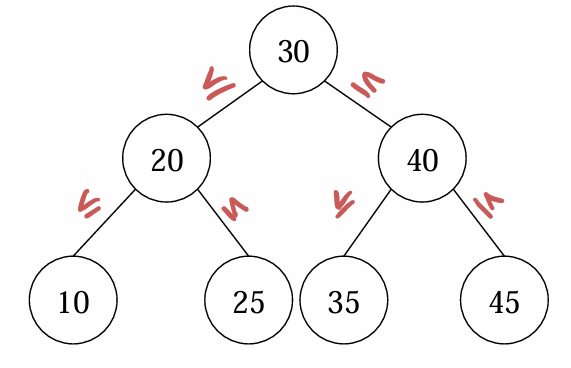

이진 탐색 트리 확인하기
트리의 Inorder Traversal의 결과가 오름차순이라면 그 트리는 이진 탐색 트리다.
이진 탐색 트리에 사용할 노드
기존에 사용할 노드와 비슷하나, 이후 Successor를 찾는 과정에서 부모로 이동하므로 부모를 가리키는 parent 멤버를 추가했다.
template <typename T>
class TreeNode
{
public:
TreeNode(T data)
{
this->data = data;
}
T data;
TreeNode<T>* left = nullptr;
TreeNode<T>* right = nullptr;
TreeNode<T>* parent = nullptr;
};이진 탐색 트리의 탐색
이진 탐색 트리에서 특정 노드를 찾으려면 반복 또는 재귀 두 가지 방법이 있다.
탐색 방식은 두 방법 모두 같다. 루트 노드에서 시작해 만나는 노드마다 찾는 값과 비교한다.
- 현재 노드의 값이 찾는 값보다 크다면 왼쪽 자식 노드로 이동
- 현재 노드의 값이 찾는 값보다 작다면 오른쪽 자식 노드로 이동
- 현재 노드의 값이 찾는 값과 같다면 해당 노드 리턴
반복(Iterative)
TreeNode<T>* FindNode_Iterative(const T& value)
{
TreeNode<T>* currNode = root;
while (currNode)
{
if (currNode->data > value)
{
std::cout << currNode->data << "\n";
currNode = currNode->left;
}
else if (currNode->data < value)
{
std::cout << currNode->data << "\n";
currNode = currNode->right;
}
else
return currNode;
}
return nullptr; // 찾지 못한 경우 nullptr 리턴
}재귀(Recursive)
// value 값 가지는 노드 리턴
TreeNode<T>* FindNode_Recursive(TreeNode<T>* node, const T& value)
{
if (node == nullptr)
return nullptr;
if (node->data > value)
{
std::cout << node->data << "\n";
return FindNode_Recursive(node->left, value);
}
else if (node->data < value)
{
std::cout << node->data << "\n";
return FindNode_Recursive(node->right, value);
}
else
return node;
}이진 탐색 트리의 최대/최솟값
최솟값
루트에서 시작해 왼쪽 자식 노드로 계속 타고 내려가면 최솟값을 가지는 노드를 찾을 수 있다.
TreeNode<T>* MinNode(TreeNode<T>* node)
{
TreeNode<T>* currNode = node;
TreeNode<T>* prevNode = nullptr;
while (currNode)
{
prevNode = currNode;
currNode = currNode->left;
}
return prevNode;
}최댓값
루트에서 시작해 오른쪽 자식 노드로 계속 타고 내려가면 최댓값을 가지는 노드를 찾을 수 있다.
TreeNode<T>* MaxNode(TreeNode<T>* node)
{
TreeNode<T>* currNode = node;
TreeNode<T>* prevNode = nullptr;
while (currNode)
{
prevNode = currNode;
currNode = currNode->right;
}
return prevNode;
}
Successor
Successor 개요
- 노드 x의 Successor란 KEY[x]보다 크면서 가장 작은 KEY를 가진 노드이다.
- 쉽게 말하자면, 어떤 노드 x보다 큰 노드 중 가장 작은 노드가 Successor가 된다.
- Successor를 찾는 방법은 두 가지가 있다.
- Inorder Traversal로 찾는 방법
- 이진 탐색 트리의 구조를 이용해 찾는 방법
Successor 찾기 (이진 탐색 트리 구조 이용)
- 노드 x가 있을 때
- 오른쪽 서브트리가 존재할 경우 오른쪽 서브트리의 최솟값이 x의 successor
- 오른쪽 서브트리가 없는 경우 x의 조상 중 다른 조상의 왼쪽 자식이 되는 노드가 successor

// node의 successor를 리턴
// 노드 x의 successor y => x보다 큰 노드 중 가장 작은 노드
TreeNode<T>* GetSuccessor(TreeNode<T>* node)
{
if (node->right) // 오른쪽 서브트리가 있는 경우
return MinNode(node->right); // 오른쪽 서브트리 최솟값
// 오른쪽 서브트리가 없는 경우 -> 왼쪽 자식이 나의 조상인 관계 찾기
TreeNode<T>* currNode = node;
TreeNode<T>* prevNode = currNode;
std::cout << "Find Successor: ";
while (currNode)
{
if (currNode->left == prevNode) // 왼쪽 자식이 node의 조상인 경우
{
std::cout << "\n";
return prevNode; // prevNode가 successor
}
std::cout << currNode->data << " ";
prevNode = currNode;
currNode = currNode->parent; // 위로 올라감
}
std::cout << "\nCouldn't find node\n";
return node; // 아무 것도 찾지 못한 경우 입력 노드 리턴
}이진 탐색 트리 노드 삽입
새롭게 노드를 삽입하는 경우, 루트에서 시작해 새로 삽입할 노드의 값과 기존 노드의 값을 비교하며 자신의 위치를 찾아간 후 그 위치에 들어가면 된다.

// 삽입
void Insert(const T& value)
{
TreeNode<T>* newNode = new TreeNode<T>(value);
TreeNode<T>* currNode = root;
// 트리가 비어있는 경우 루트로 설정
if (root == nullptr)
{
root = newNode;
return;
}
while (currNode)
{
if (currNode->data > value) // 왼쪽 이동
{
if (currNode->left == nullptr) // 비어있는 경우 그 자리에 삽입
{
currNode->left = newNode;
newNode->parent = currNode;
return;
}
else
currNode = currNode->left;
}
else if (currNode->data < value) // 오른쪽 이동
{
if (currNode->right == nullptr) // 비어있는 경우 그 자리에 삽입
{
currNode->right = newNode;
newNode->parent = currNode;
return;
}
else
currNode = currNode->right;
}
else
{
std::cout << "Node already exists!\n";
delete newNode;
return;
}
}
}
이진 탐색 트리 노드 삭제
이진 탐색 트리에서 노드를 삭제할 때 삭제할 노드의 자식 노드 개수에 따라 세 가지 경우가 있는데, 각각 다르게 처리 해줘야 한다.
자식 노드가 없는 경우
노드를 바로 삭제하고, 부모 노드의 자식 포인터를 nullptr로 설정해준다.

자식 노드가 1개인 경우
자신의 부모와 자식을 연결해준 후, 노드를 삭제한다.

자식 노드가 2개인 경우(중요)
- 삭제할 노드의 Successor를 찾는다. (자식이 2개이므로 오른쪽 서브트리가 무조건 있음) (오른쪽 서브트리 중 가장 작은 노드가 삭제할 노드의 위치에 와야 문제가 생기지 않으므로 Successor를 찾음)
- Successor를 잠시 빼낸다. 이때, Successor의 자식 개수(0개 또는 1개)에 따라 알맞게 처리한다.
- 삭제할 노드의 위치에 Successor를 덮어 씌운다.

5의 Successor는 6이 된다.
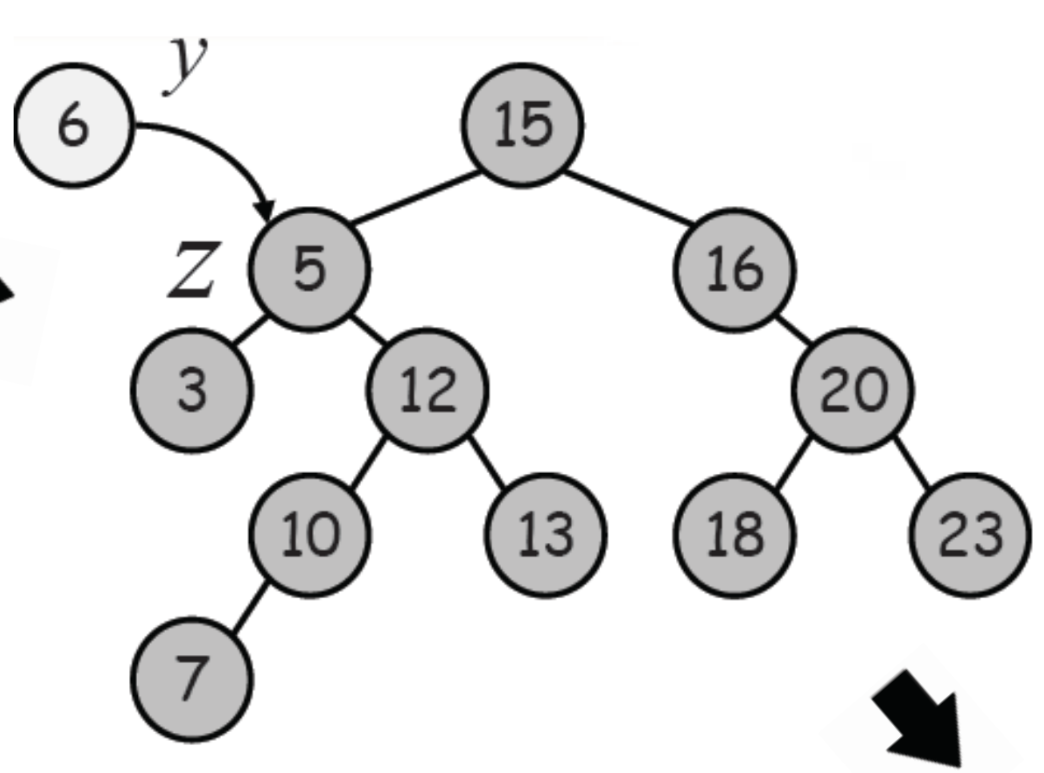
Successor의 자식 개수에 따라 알맞게 처리한 후, 기존 5의 위치에 Successor를 덮어 씌운다.

void Remove(TreeNode<T>* node)
{
// 1. 삭제할 노드 파악
// 자식 노드가 2개인 경우 Successor, 1개 이하인 경우 node를 삭제
TreeNode<T>* delNode = nullptr;
if (node->left == nullptr || node->right == nullptr) // 자식 노드 1개 이하
delNode = node;
else // 자식 노드 2개
delNode = GetSuccessor(node);
// 2. 삭제할 노드의 자식 노드 파악
TreeNode<T>* child = nullptr;
if (delNode->left != nullptr) // 삭제할 노드의 자식 노드 저장
child = delNode->left;
else
child = delNode->right;
// 3. 자식 노드가 있는 경우 자신의 부모와 이어줌
if (child != nullptr) // 부모 관계 재설정
child->parent = delNode->parent;
// 4. 부모 노드에서의 자식 노드 위치를 결정
// 삭제할 노드가 있는 자리를 파악
if (delNode->parent == nullptr) // 루트 노드를 지우는 경우
root = child;
else if (delNode == delNode->parent->left)
delNode->parent->left = child;
else
delNode->parent->right = child;
// 5. delNode가 successor인 경우 원래 삭제하려고 했던 노드 위치에 successor를 덮어 씌움
if (delNode != node)
node->data = delNode->data;
delete delNode;
}이진 탐색 트리 전체 코드
더보기
#include <iostream>
template <typename T>
class TreeNode
{
public:
TreeNode(T data)
{
this->data = data;
}
T data;
TreeNode<T>* left = nullptr;
TreeNode<T>* right = nullptr;
TreeNode<T>* parent = nullptr;
};
template <typename T>
class BinarySearchTree
{
public:
void Inorder(TreeNode<T>* node)
{
if (node)
{
Inorder(node->left);
std::cout << node->data << " ";
Inorder(node->right);
}
}
// value 값 가지는 노드 리턴
TreeNode<T>* FindNode_Recursive(TreeNode<T>* node, const T& value)
{
if (node == nullptr)
return nullptr;
if (node->data > value)
{
std::cout << node->data << "\n";
return FindNode_Recursive(node->left, value);
}
else if (node->data < value)
{
std::cout << node->data << "\n";
return FindNode_Recursive(node->right, value);
}
else
return node;
}
TreeNode<T>* FindNode_Iterative(const T& value)
{
TreeNode<T>* currNode = root;
while (currNode)
{
if (currNode->data > value)
{
std::cout << currNode->data << "\n";
currNode = currNode->left;
}
else if (currNode->data < value)
{
std::cout << currNode->data << "\n";
currNode = currNode->right;
}
else
return currNode;
}
return nullptr; // 찾지 못한 경우 nullptr 리턴
}
// 삽입
void Insert(const T& value)
{
TreeNode<T>* newNode = new TreeNode<T>(value);
TreeNode<T>* currNode = root;
// 트리가 비어있는 경우 루트로 설정
if (root == nullptr)
{
root = newNode;
return;
}
while (currNode)
{
if (currNode->data > value) // 왼쪽 이동
{
if (currNode->left == nullptr) // 비어있는 경우 그 자리에 삽입
{
currNode->left = newNode;
newNode->parent = currNode;
return;
}
else
currNode = currNode->left;
}
else if (currNode->data < value) // 오른쪽 이동
{
if (currNode->right == nullptr) // 비어있는 경우 그 자리에 삽입
{
currNode->right = newNode;
newNode->parent = currNode;
return;
}
else
currNode = currNode->right;
}
else
{
std::cout << "Node already exists!\n";
delete newNode;
return;
}
}
}
TreeNode<T>* GetRoot()
{
return root;
}
void SetRoot(TreeNode<T>* node)
{
root = node;
}
TreeNode<T>* MinNode(TreeNode<T>* node)
{
TreeNode<T>* currNode = node;
TreeNode<T>* prevNode = nullptr;
while (currNode)
{
prevNode = currNode;
currNode = currNode->left;
}
return prevNode;
}
TreeNode<T>* MaxNode(TreeNode<T>* node)
{
TreeNode<T>* currNode = node;
TreeNode<T>* prevNode = nullptr;
while (currNode)
{
prevNode = currNode;
currNode = currNode->right;
}
return prevNode;
}
// node의 successor를 리턴
// 노드 x의 successor y => x보다 큰 노드 중 가장 작은 노드
TreeNode<T>* GetSuccessor(TreeNode<T>* node)
{
if (node->right) // 오른쪽 서브트리가 있는 경우
return MinNode(node->right); // 오른쪽 서브트리 최솟값
// 오른쪽 서브트리가 없는 경우 -> 왼쪽 자식이 나의 조상인 관계 찾기
TreeNode<T>* currNode = node;
TreeNode<T>* prevNode = currNode;
std::cout << "Find Successor: ";
while (currNode)
{
if (currNode->left == prevNode) // 왼쪽 자식이 node의 조상인 경우
{
std::cout << "\n";
return prevNode; // prevNode가 successor
}
std::cout << currNode->data << " ";
prevNode = currNode;
currNode = currNode->parent; // 위로 올라감
}
std::cout << "\nCouldn't find node\n";
return node; // 아무 것도 찾지 못한 경우 입력 노드 리턴
}
void Remove(TreeNode<T>* node)
{
TreeNode<T>* delNode = nullptr;
if (node->left == nullptr || node->right == nullptr) // 자식 노드 1개 이하
delNode = node;
else // 자식 노드 2개
delNode = GetSuccessor(node);
TreeNode<T>* child = nullptr;
if (delNode->left != nullptr) // 삭제할 노드의 자식 노드 저장
child = delNode->left;
else
child = delNode->right;
if (child != nullptr) // 부모 관계 재설정
child->parent = delNode->parent;
// 자식 위치 결정
if (delNode->parent == nullptr) // 루트 노드를 지우는 경우
root = child;
else if (delNode == delNode->parent->left)
delNode->parent->left = child;
else
delNode->parent->right = child;
// delNode가 successor인 경우
if (delNode != node)
node->data = delNode->data;
delete delNode;
}
private:
TreeNode<T>* root = nullptr;
};728x90
'Programming > Algorithm & Data Structure' 카테고리의 다른 글
| [Data Structure] 신장 트리, 최소 비용 신장 트리와 Kruskal, Prim 알고리즘 (0) | 2025.01.13 |
|---|---|
| [Data Structure] 그래프와 기본 연산 (BFS, DFS) (0) | 2025.01.13 |
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2025.01.13 |
| [Data Structure] 힙 트리 (0) | 2025.01.13 |
| [Data Structure] 이진 트리 순회 (0) | 2025.01.13 |
