728x90
신장 트리 (Spanning Tree)
그래프 상의 모든 정점이 사이클 없이 연결된 부분 그래프를 신장 트리라 한다.
정점의 개수가 n개인 경우, 신장 트리는 n-1개의 간선을 가진다.

최소 비용 신장 트리 (Minimum-cost Spanning Tree, MST)
주어진 그래프에서 모든 정점을 연결하는 트리 중 간선 가중치의 합이 최소인 트리
가중치가 있는 무방향 그래프의 신장 트리의 비용은 신장 트리에 있는 간선들의 비용(가중치)의 합이다.
신장 트리의 비용이 최소가 되는 트리를 최소 비용 신장 트리(MST)라 한다.
MST를 구성하는 데에는 다음의 제한 조건이 있다.
- 그래프 내에 있는 간선만 사용
- 정확하게 n-1개의 간선만 사용
- 사이클을 생성하는 간선은 사용하지 않음
MST를 구하기 위해선 대표적으로 세 가지 알고리즘이 있는데, 모두 그리디 알고리즘이다.
이 게시물에선 Kruskal와 Prim 알고리즘만 알아본다.
Union-Find와 Kruskal 알고리즘
Kruskal 알고리즘은 서로소 집합을 사용한다.
서로소 집합
- 트리를 사용해 집합을 표현할 수 있는 방법이 있다.
- 어떠한 원소도 공통으로 가지고 있지 않은 두 집합을 서로소 집합이라 한다.
- 여러 정점을 하나의 집합으로 묶으려면, 대표가 되는 하나의 정점 다른 정점들이 모두 가리키게 하면 된다.

- 이러한 집합에 수행하고자 하는 연산은 다음과 같다
- 합집합(Union): 서로소 집합인 두 집합을 합침
- 탐색(Find): 원소 i를 포함하는 집합 탐색
- 이를 나타내기 위해 각 원소의 부모를 나타내는 parent 배열을 사용
- parent 배열의 값이 -1이면 대표 노드
Union-Find 알고리즘
- 합집합(Union) 연산
- 두 트리 중 하나를 다른 트리의 서브 트리로 만들면 된다.
- 다른 서브 트리의 대표 원소의 parent 값을 어떤 트리의 대표 원소로 바꾼다.
// u가 속한 집합을 v가 속한 집합에 합침
void Union(int u, int v)
{
int uRoot = Find(u);
int vRoot = Find(v);
if (uRoot != vRoot)
parent[uRoot] = v;
}- 탐색(Find) 연산
- 두 노드의 parent가 같은 지 확인하면 된다.
- parent를 확인하려면 -1이 나올 때까지 계속 올라가면 된다.
// u가 속한 집합의 대표 원소를 리턴
int Find(int u)
{
while (parent[u] >= 0)
{
u = parent[u];
}
return u;
}서로소 집합 클래스의 전체 코드는 다음과 같다.
#pragma once
#include <algorithm>
class DisjointSet
{
public:
DisjointSet(int elemNum)
{
n = elemNum;
parent = new int[n];
std::fill(parent, parent + n, -1); // parent 배열 -1로 채우기 -> 처음엔 모든 원소가 각각의 서로소 집합에 포함
}
// u가 속한 집합의 대표 원소를 리턴
int Find(int u)
{
while (parent[u] >= 0)
{
u = parent[u];
}
return u;
}
// u가 속한 집합을 v가 속한 집합에 합침
void Union(int u, int v)
{
int uRoot = Find(u);
int vRoot = Find(v);
if (uRoot != vRoot)
parent[uRoot] = v;
}
// 같은 집합 안에 있는지 여부
bool IsInSameSet(int u, int v)
{
int uRoot = Find(u);
int vRoot = Find(v);
if (uRoot == vRoot)
return true;
else
return false;
}
private:
int* parent; // parent 배열
int n; // 집합 원소 개수
};Kruskal 알고리즘
- 모든 간선에 대한 정보를 리스트에 저장한 후, 가중치를 기준으로 오름차순으로 정렬한다.
- 가중치가 작은 간선부터 선택하며 n-1개를 선택할 때까지 다음을 반복한다
- 만약 새롭게 추가할 간선이 사이클을 이루지 않고 있다면(간선으로 연결될 두 정점이 서로소 집합이면) 두 정점이 속한 집합을 합치고 해당 간선을 선택 리스트에 저장한다.
- 만약 사이클을 이룬다면 다음 간선으로 스킵한다.

https://aditya-yadav.medium.com/kruskals-algorithm-for-minimum-spanning-tree-f3c0c0b7b386
// 크루스칼 알고리즘
void Kruskal()
{
int weightSum = 0;
DisjointSet* set = new DisjointSet(n); // 서로소 집합 생성
std::sort(edges.begin(), edges.end()); // 가중치 순서대로 정렬
std::vector<Edge> selected; // 선택한 간선 집합
while (selected.size() < n-1 && !edges.empty()) // n-1개의 간선을 선택
{
Edge minEdge = edges.front();
edges.erase(edges.begin()); // 맨 앞에서 삭제
if (!set->IsInSameSet(minEdge.u, minEdge.v)) // 두 정점이 사이클을 이루지 않고 있다면
{
set->Union(minEdge.u, minEdge.v); // 두 집합 합치기
selected.push_back(minEdge); // selected 벡터에 추가
weightSum += minEdge.weight;
}
}
// 결과 출력
for (auto iter = selected.begin(); iter != selected.end(); ++iter)
std::cout << iter->u << " - " << iter->v << "\n";
std::cout << "Cost: " << weightSum << "\n";
delete set;
}Prim 알고리즘
Prim 알고리즘
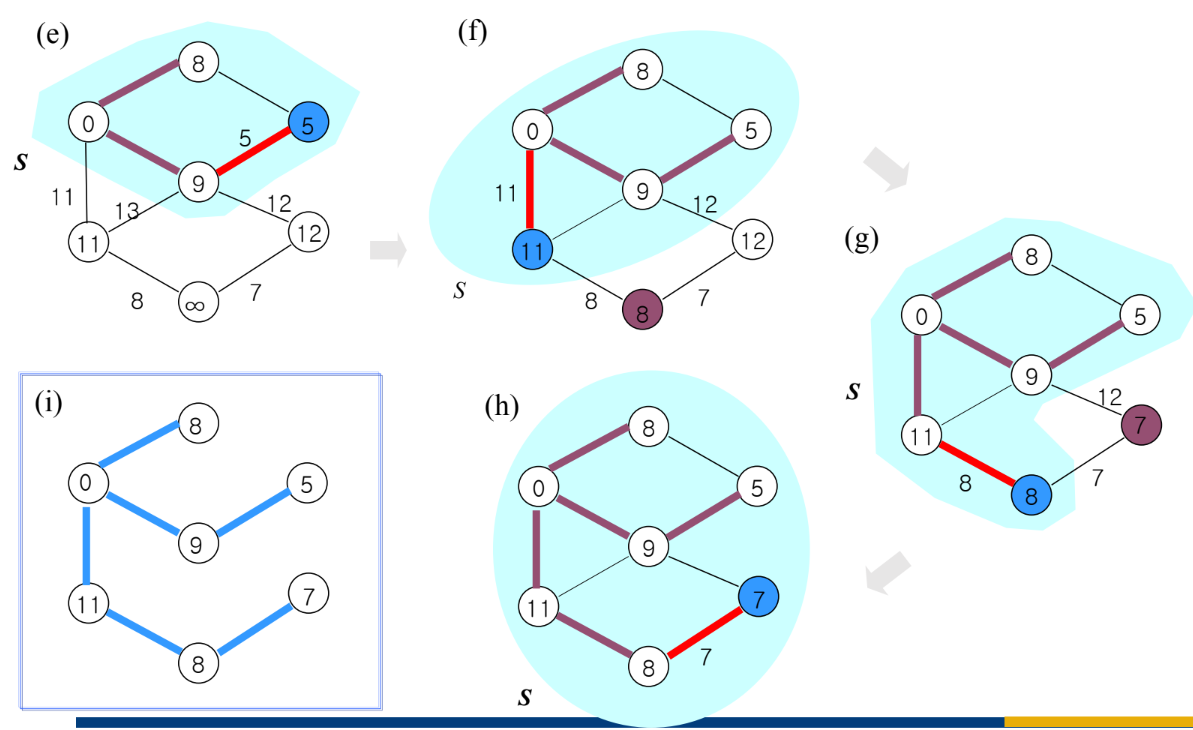
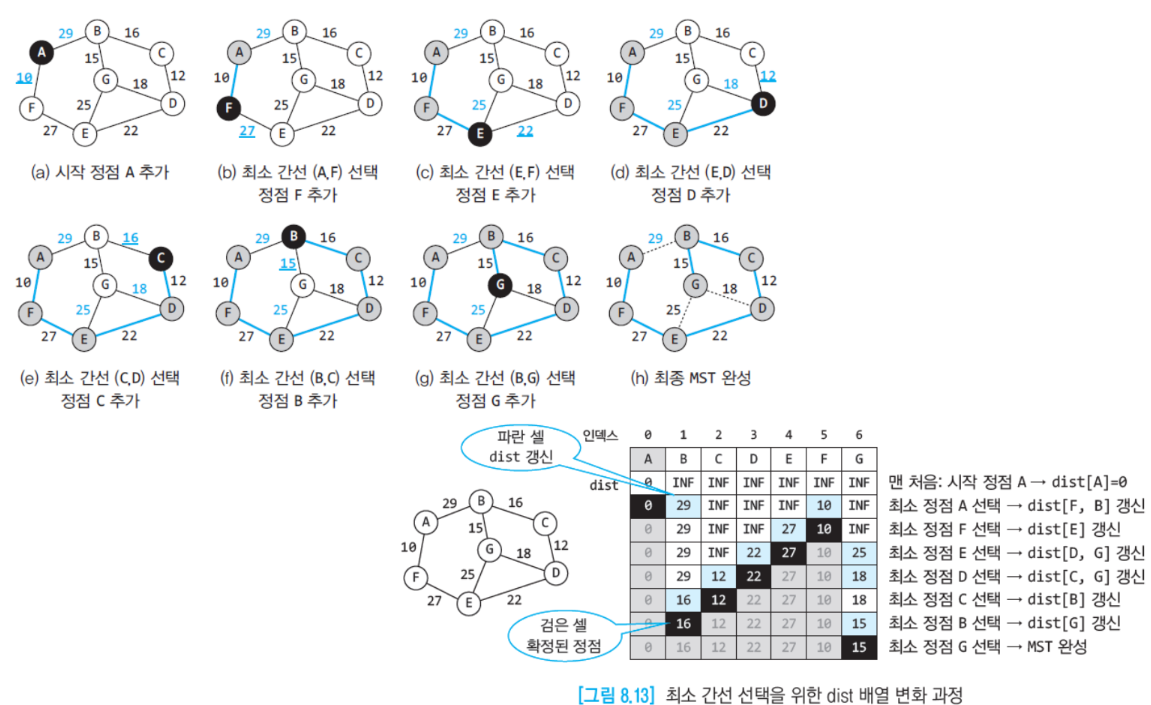
Prim 알고리즘은 특정 정점에서 시작한다. n-1개의 간선을 선택하기 전까지 다음을 반복한다.
- 현재 정점에서 이동 가능한 정점들에 대해 거리 정보를 업데이트 한다. (이를 Relaxation이라 함)
- 사용 가능한 간선 중 가중치가 가장 작은 간선을 선택한다. (이전에 찾은 간선이여도 됨)
- 해당 간선으로 이동할 정점에 대해 방문처리를 한 후 이동한다.

// 발견했으나 방문하지 않은 정점 중 가장 가까운 정점 리턴
virtual Edge GetMinVertex(int u, bool* visited, bool* found)
{
int minW = INF;
int minV = 0;
for (int i = 0; i < n; i++)
{
if (i == u) continue; // 자기 자신은 스킵
if (found[i] && !visited[i]) // 발견했는데 방문하지 않은 정점이고
{
if (dist[i] < minW) // 가중치가 가장 작은 것을 찾으면
{
minW = dist[i];
minV = i;
}
}
}
std::cout << "Min: " << u << " " << minV << " " << minW << "\n";
return {u, minV, minW};
}
void Prim(int v)
{
int weightSum = 0;
bool* visited = new bool[n + 1]; // 방문한 정점
bool* found = new bool[n + 1]; // 발견한 정점
std::fill(visited, visited + n + 1, false);
std::fill(found, found + n + 1, false);
std::fill(dist, dist + n + 1, INF); // 거리 배열 초기화
dist[v] = 0; // 시작 정점 거리 설정
visited[v] = true; // 시작 정점 방문 처리
found[v] = true; // 시작 정점 발견 처리
int visitedCnt = 1;
while (visitedCnt < n) // n-1개의 간선을 선택할 때까지
{
Relaxation(v, visited, found);
Edge closestEdge = GetMinVertex(v, visited, found); // v와 인접한 정점 중 가장 가까운 정점으로 연결되는 간선
visited[closestEdge.v] = true; // 방문 처리
visitedCnt++;
weightSum += closestEdge.weight;
std::cout << v << " - " << closestEdge.v << "\n";
v = closestEdge.v;
}
std::cout << "Weight: " << weightSum << "\n";
delete visited;
delete found;
}
인접 행렬 / 리스트에 따라 Relaxation 코드가 달라진다.
Relaxation - 인접 행렬
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation(int v, bool* visited, bool* found)
{
for (int i = 0; i < n; i++)
{
if (i == v) continue; // 자기 자신이면 스킵
if (adjMatrix[v][i] == 0) continue; // 간선 존재하지 않으면 스킵
if (!visited[i]) // 방문하지 않은 정점이고
{
if (adjMatrix[v][i] < dist[i]) // 더 짧은 거리를 찾았으면
dist[i] = adjMatrix[v][i]; // 거리 업데이트
found[i] = true; // 발견 여부 업데이트
}
}
}Relaxation - 인접 리스트
virtual void Relaxation(int v, bool* visited, bool* found)
{
BidirectionalNode<int>* curr = adjList[v].head->right;
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았고
{
if (curr->weight < dist[curr->data]) // 기존에 알고 있던 거리보다 더 짧은 경로가 있으면
dist[curr->data] = curr->weight; // 거리 업데이트
found[curr->data] = true; // 발견 여부 저장
}
curr = curr->right;
}
}전체 코드
더보기
// Graph.hpp
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
#include "../5.10/DisjointSet.hpp"
#include "Edge.hpp"
#define INF 99999999
class Graph
{
public:
virtual ~Graph()
{
delete dist; // 거리 배열 삭제
}
// 그래프에 정점이 없으면 true 리턴
bool IsEmpty() const
{
return n == 0;
}
// 정점 수 리턴
int NumberOfVertices() const
{
return n;
}
// 간선 수 리턴
int NumberOfEdges() const
{
return e;
}
// 정점 u에 인접한 간선 수 리턴
virtual int Degree(int u) const = 0; // 순수 가상 함수
// 그래프에 간선 (u,v)가 있으면 true 리턴
virtual bool ExistsEdge(int u, int v) const = 0;
// 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v) = 0;
// 가중치 w인 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v, int w) = 0;
// 그래프에서 간선 (u,v) 삭제
virtual void DeleteEdge(int u, int v) = 0;
// 크루스칼 알고리즘
void Kruskal()
{
int weightSum = 0;
DisjointSet* set = new DisjointSet(n); // 서로소 집합 생성
std::sort(edges.begin(), edges.end()); // 가중치 순서대로 정렬
std::vector<Edge> selected; // 선택한 간선 집합
while (selected.size() < n-1 && !edges.empty()) // n-1개의 간선을 선택
{
Edge minEdge = edges.front();
edges.erase(edges.begin()); // 맨 앞에서 삭제
if (!set->IsInSameSet(minEdge.u, minEdge.v)) // 두 정점이 사이클을 이루지 않고 있다면
{
set->Union(minEdge.u, minEdge.v); // 두 집합 합치기
selected.push_back(minEdge); // selected 벡터에 추가
weightSum += minEdge.weight;
}
}
// 결과 출력
for (auto iter = selected.begin(); iter != selected.end(); ++iter)
std::cout << iter->u << " - " << iter->v << "\n";
std::cout << "Cost: " << weightSum << "\n";
delete set;
}
// 발견했으나 방문하지 않은 정점 중 가장 가까운 정점 리턴
virtual Edge GetMinVertex(int u, bool* visited, bool* found)
{
int minW = INF;
int minV = 0;
for (int i = 0; i < n; i++)
{
if (i == u) continue; // 자기 자신은 스킵
if (found[i] && !visited[i]) // 발견했는데 방문하지 않은 정점이고
{
if (dist[i] < minW) // 가중치가 가장 작은 것을 찾으면
{
minW = dist[i];
minV = i;
}
}
}
std::cout << "Min: " << u << " " << minV << " " << minW << "\n";
return {u, minV, minW};
}
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation(int v, bool* visited, bool* found) = 0;
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation_Dijkstra(int v, bool* visited, bool* found) = 0;
void Prim(int v)
{
int weightSum = 0;
bool* visited = new bool[n + 1]; // 방문한 정점
bool* found = new bool[n + 1]; // 발견한 정점
std::fill(visited, visited + n + 1, false);
std::fill(found, found + n + 1, false);
std::fill(dist, dist + n + 1, INF); // 거리 배열 초기화
dist[v] = 0; // 시작 정점 거리 설정
visited[v] = true; // 시작 정점 방문 처리
found[v] = true; // 시작 정점 발견 처리
int visitedCnt = 1;
while (visitedCnt < n) // n-1개의 간선을 선택할 때까지
{
Relaxation(v, visited, found);
Edge closestEdge = GetMinVertex(v, visited, found); // v와 인접한 정점 중 가장 가까운 정점으로 연결되는 간선
visited[closestEdge.v] = true; // 방문 처리
visitedCnt++;
weightSum += closestEdge.weight;
std::cout << v << " - " << closestEdge.v << "\n";
v = closestEdge.v;
}
std::cout << "Weight: " << weightSum << "\n";
delete visited;
delete found;
}
protected:
int n; // 정점의 수
int e; // 간선의 수
std::vector<Edge> edges; // 모든 간선 집합
int* dist; // 거리 배열
};// MatrixWGraph.hpp
#include "Graph.hpp"
class MatrixWGraph : public Graph
{
public:
MatrixWGraph(int vertexCnt)
{
n = vertexCnt; // 정점 개수 설정
e = 0; // 간선 개수 설정
// 이차원 배열 동적 할당
adjMatrix = new int*[n + 1];
for (int i = 0; i <= n; i++)
{
adjMatrix[i] = new int[n + 1];
std::fill(adjMatrix[i], adjMatrix[i] + n + 1, 0); // 0으로 채우기
}
dist = new int[n + 1]; // 거리 배열 할당
}
~MatrixWGraph()
{
for (int i = 0; i <= n; i++)
{
delete adjMatrix[i];
}
delete adjMatrix;
delete dist; // 거리 배열 삭제
}
void PrintAdjMatrix()
{
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
std::cout << adjMatrix[i][j] << " ";
}
std::cout << "\n";
}
}
// 정점 u에 인접한 간선 수 리턴
virtual int Degree(int u) const
{
int edgeCnt = 0;
for (int i = 0; i < n+1; i++)
{
if (adjMatrix[u][i] != 0)
edgeCnt++;
}
return edgeCnt;
}
// 그래프에 간선 (u,v)가 있으면 true 리턴
virtual bool ExistsEdge(int u, int v) const
{
if (adjMatrix[u][v] != 0)
return true;
else
return false;
}
// 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v)
{
adjMatrix[u][v] = 1; // 무방향 그래프
adjMatrix[v][u] = 1;
edges.push_back({u, v, 1}); // 간선 리스트 추가
}
// 가중치가 w인 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v, int w)
{
adjMatrix[u][v] = w; // 무방향 그래프
adjMatrix[v][u] = w;
edges.push_back({u, v, w}); // 간선 리스트 추가
}
// 그래프에서 간선 (u,v) 삭제
virtual void DeleteEdge(int u, int v)
{
adjMatrix[u][v] = 0; // 무방향 그래프
adjMatrix[v][u] = 0;
}
void DFSWrapper(int v)
{
bool* visited = new bool[n + 1];
DFS(v, visited);
delete visited;
}
void DFS(int v, bool* visited)
{
visited[v] = true;
std::cout << v << " ";
for(int i = 0; i <= n; i++)
{
if (adjMatrix[v][i] && !visited[i]) // 인접한 정점 중 방문하지 않은 정점이 있으면
DFS(i, visited);
}
}
void BFS(int v)
{
bool* visited = new bool[n + 1];
std::queue<int> q;
// 시작 정점 큐에 추가
q.push(v);
visited[v] = true;
while (!q.empty())
{
int front = q.front();
q.pop();
std::cout << front << " ";
for (int i = 0; i <= n; i++)
{
if (adjMatrix[front][i] && !visited[i]) // 인접한 정점 중 방문하지 않은 정점이 있다면
{
q.push(i);
visited[i] = true; // 방문 처리
}
}
}
delete visited;
}
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation(int v, bool* visited, bool* found)
{
for (int i = 0; i < n; i++)
{
if (i == v) continue; // 자기 자신이면 스킵
if (adjMatrix[v][i] == 0) continue; // 간선 존재하지 않으면 스킵
if (!visited[i]) // 방문하지 않은 정점이고
{
if (adjMatrix[v][i] < dist[i]) // 더 짧은 거리를 찾았으면
dist[i] = adjMatrix[v][i]; // 거리 업데이트
found[i] = true; // 발견 여부 업데이트
}
}
}
private:
int** adjMatrix; // 인접 행렬
};// LinkedWGraph.hpp
#include "Graph.hpp"
#include "../../Chapter4/4.10/DoublyLinkedList.hpp"
class LinkedWGraph : public Graph
{
public:
LinkedWGraph(int vertexCnt)
{
n = vertexCnt; // 정점 개수 설정
e = 0;
adjList = new DoublyLinkedList<int>[n]; // 인접 리스트 할당
for (int i = 0; i <= n; i++)
{
adjList[i].head = new BidirectionalNode<int>(i);
}
dist = new int[n + 1]; // 거리 배열 할당
}
~LinkedWGraph()
{
delete adjList; // 인접 리스트 삭제
}
void PrintAdjList()
{
for (int i = 0; i <= n; i++)
{
std::cout << i << ": ";
BidirectionalNode<int>* curr = adjList[i].head->right;
while (curr)
{
std::cout << curr->data << " -> ";
curr = curr->right;
}
std::cout << "nullptr\n";
}
}
// 정점 u에 인접한 간선 수 리턴
virtual int Degree(int u) const
{
int edgeCnt = 0;
BidirectionalNode<int>* curr = adjList[u].head->right; // 뒤에 연결된 인접한 정점부터 시작
while (curr)
{
edgeCnt++;
curr = curr->right;
}
return edgeCnt;
}
// 그래프에 간선 (u,v)가 있으면 true 리턴
virtual bool ExistsEdge(int u, int v) const
{
BidirectionalNode<int>* curr = adjList[u].head;
while (curr)
{
if (curr->data == v) // 연결된 인접 정점 중 v가 있으면
return true;
curr = curr->right;
}
return false; // 없는 경우
}
// 간선 (u,v)를 그래프에 삽입
// 양방향 그래프이므로 양쪽에 삽입
virtual void InsertEdge(int u, int v)
{
BidirectionalNode<int>* uVert = new BidirectionalNode<int>(u); // 새로운 정점 노드
BidirectionalNode<int>* vVert = new BidirectionalNode<int>(v);
adjList[u].Insert(vVert, adjList[u].GetLastNode()); // 리스트 맨 뒤에 추가
adjList[v].Insert(uVert, adjList[v].GetLastNode());
edges.push_back({u, v, 1});
}
// 가중치가 w인 간선 (u,v)를 그래프에 삽입
// 양방향 그래프이므로 양쪽에 삽입
virtual void InsertEdge(int u, int v, int w)
{
BidirectionalNode<int>* uVert = new BidirectionalNode<int>(u, w); // 새로운 정점 노드
BidirectionalNode<int>* vVert = new BidirectionalNode<int>(v, w);
adjList[u].Insert(vVert, adjList[u].GetLastNode()); // 리스트 맨 뒤에 추가
adjList[v].Insert(uVert, adjList[v].GetLastNode());
edges.push_back({u, v, w});
}
// 그래프에서 간선 (u,v) 삭제
virtual void DeleteEdge(int u, int v)
{
BidirectionalNode<int>* vNode = adjList[u].Find(v);
adjList[u].Delete(vNode);
}
// DFS
void DFSWrapper(int v)
{
bool* visited = new bool[n + 1];
DFS(v, visited);
delete visited;
}
void DFS(int v, bool* visited)
{
visited[v] = true; // 방문 처리
std::cout << v << " ";
BidirectionalNode<int>* curr = adjList[v].head->right; // 인접한 정점의 노드부터 시작
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았으면
DFS(curr->data, visited);
curr = curr->right;
}
}
// BFS
void BFS(int v)
{
bool* visited = new bool[n + 1];
std::queue<int> q;
// 시작 정점 큐에 추가
q.push(v);
visited[v] = true;
while (!q.empty())
{
int front = q.front();
q.pop();
std::cout << front << " ";
BidirectionalNode<int>* curr = adjList[front].head->right; // 인접한 정점의 노드부터 시작
while (curr)
{
if (!visited[curr->data]) // 인접한 정점 중 방문 안 한 노드가 있으면
{
q.push(curr->data); // 큐 추가
visited[curr->data] = true; // 방문 처리
}
curr = curr->right;
}
}
delete visited;
}
virtual void Relaxation(int v, bool* visited, bool* found)
{
BidirectionalNode<int>* curr = adjList[v].head->right;
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았고
{
if (curr->weight < dist[curr->data]) // 기존에 알고 있던 거리보다 더 짧은 경로가 있으면
dist[curr->data] = curr->weight; // 거리 업데이트
found[curr->data] = true; // 발견 여부 저장
}
curr = curr->right;
}
}
private:
DoublyLinkedList<int>* adjList;
};728x90
'Programming > Algorithm & Data Structure' 카테고리의 다른 글
| [Data Structure] AVL 트리 (0) | 2025.01.18 |
|---|---|
| [Algorithm] 최단 경로 - Dijkstra 알고리즘 (0) | 2025.01.13 |
| [Data Structure] 그래프와 기본 연산 (BFS, DFS) (0) | 2025.01.13 |
| [Data Structure] 이진 탐색 트리 (0) | 2025.01.13 |
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2025.01.13 |
