728x90
최단 경로
그래프에서의 최단 경로 문제는 방향 그래프를 기준으로 구한다.
음이 아닌 가중치 그래프의 최단 경로 (Dijkstra 알고리즘)
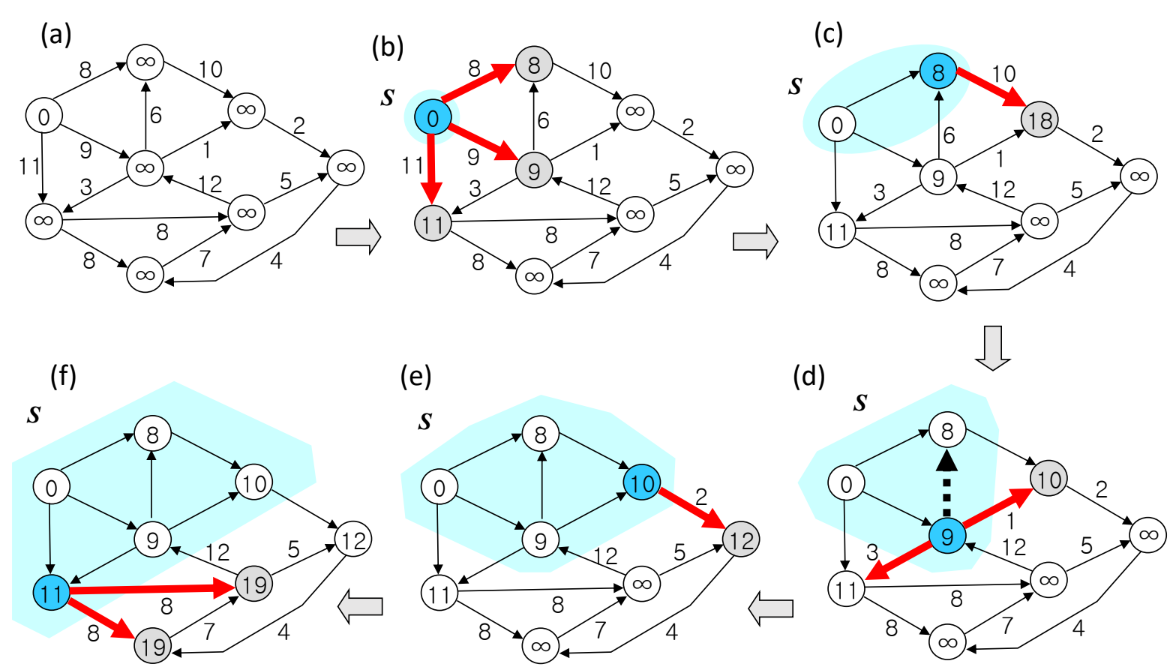
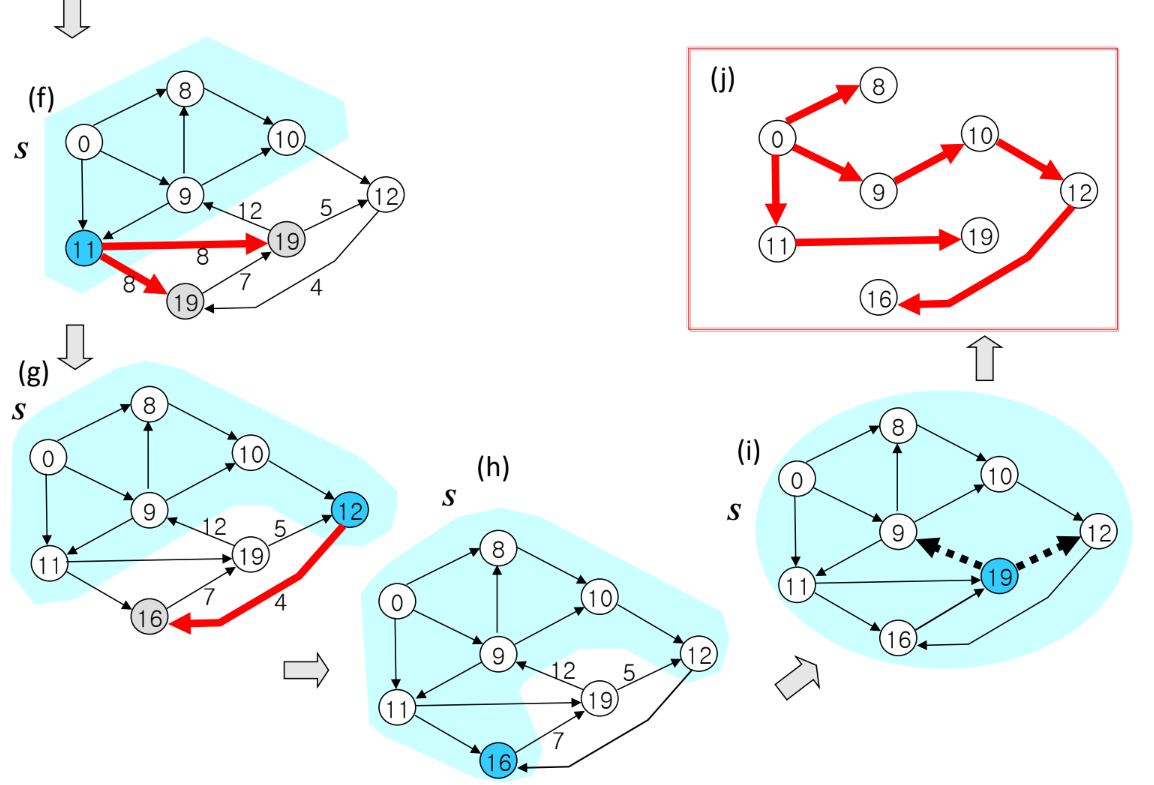
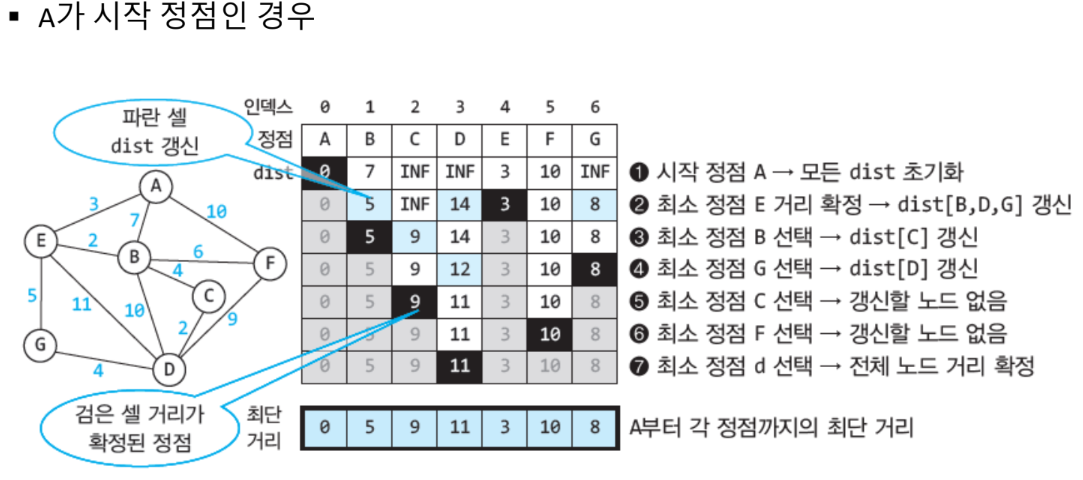
- 다익스트라(또는 데이크스트라) 알고리즘은 한 정점에서 다른 모든 정점까지의 최단 경로 거리를 구한다.
- Dijkstra 알고리즘은 기본적으로 Prim 알고리즘과 매우 유사하다.
- Dijkstra 알고리즘은 그래프의 모든 가중치가 음이 아닌 경우에만 유효하다.
- Prim 알고리즘과 Relaxation 과정만 차이가 있다.
- Prim 알고리즘은 현재 정점에서 인접한 정점까지의 새로 찾은 거리가 dist 배열에 기록된 거리보다 더 짧은 경우 업데이트
- Dijkstra 알고리즘은 현재 정점까지의 누적 거리와 인접한 어떤 정점까지의 새로 찾은 거리를 더했을 때 dist 배열에 기록된 거리보다 더 짧은 경우에만 업데이트
Relaxation - 인접 행렬
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation_Dijkstra(int v, bool* visited, bool* found)
{
for (int i = 0; i < n; i++)
{
if (i == v) continue; // 자기 자신이면 스킵
if (adjMatrix[v][i] == 0) continue; // 간선 존재하지 않으면 스킵
if (!visited[i]) // 방문하지 않은 정점이고
{
if (dist[v] + adjMatrix[v][i] < dist[i]) // 더 짧은 거리를 찾았으면
dist[i] = dist[v] + adjMatrix[v][i]; // 거리 업데이트
found[i] = true; // 발견 여부 업데이트
}
}
// 모든 정점까지 이동하는데 필요한 최단 거리 출력
std::cout << "Dist: ";
for (int i = 0; i < n; i++)
std::cout << dist[i] << " ";
std::cout << "\n";
}Relaxation - 인접 리스트
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation_Dijkstra(int v, bool* visited, bool* found)
{
BidirectionalNode<int>* vVert = adjList[v].head;
BidirectionalNode<int>* curr = vVert->right;
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았고
{
if (dist[vVert->data] + curr->weight < dist[curr->data]) // 새로 찾은 누적 경로가 dist에 담긴 거리보다 짧으면
dist[curr->data] = dist[vVert->data] + curr->weight; // 거리 업데이트
found[curr->data] = true; // 발견 여부 저장
}
curr = curr->right;
}
// 모든 정점까지 이동하는데 필요한 최단 거리 출력
std::cout << "Dist: ";
for (int i = 0; i < n; i++)
std::cout << dist[i] << " ";
std::cout << "\n";
}그래프 전체 코드
더보기
// Graph.hpp
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
#include "../5.10/DisjointSet.hpp"
#include "Edge.hpp"
#define INF 99999999
class Graph
{
public:
virtual ~Graph()
{
delete dist; // 거리 배열 삭제
}
// 그래프에 정점이 없으면 true 리턴
bool IsEmpty() const
{
return n == 0;
}
// 정점 수 리턴
int NumberOfVertices() const
{
return n;
}
// 간선 수 리턴
int NumberOfEdges() const
{
return e;
}
// 정점 u에 인접한 간선 수 리턴
virtual int Degree(int u) const = 0; // 순수 가상 함수
// 그래프에 간선 (u,v)가 있으면 true 리턴
virtual bool ExistsEdge(int u, int v) const = 0;
// 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v) = 0;
// 가중치 w인 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v, int w) = 0;
// 그래프에서 간선 (u,v) 삭제
virtual void DeleteEdge(int u, int v) = 0;
// 크루스칼 알고리즘
void Kruskal()
{
int weightSum = 0;
DisjointSet* set = new DisjointSet(n); // 서로소 집합 생성
std::sort(edges.begin(), edges.end()); // 가중치 순서대로 정렬
std::vector<Edge> selected; // 선택한 간선 집합
while (selected.size() < n-1 && !edges.empty()) // n-1개의 간선을 선택
{
Edge minEdge = edges.front();
edges.erase(edges.begin()); // 맨 앞에서 삭제
if (!set->IsInSameSet(minEdge.u, minEdge.v)) // 두 정점이 사이클을 이루지 않고 있다면
{
set->Union(minEdge.u, minEdge.v); // 두 집합 합치기
selected.push_back(minEdge); // selected 벡터에 추가
weightSum += minEdge.weight;
}
}
// 결과 출력
for (auto iter = selected.begin(); iter != selected.end(); ++iter)
std::cout << iter->u << " - " << iter->v << "\n";
std::cout << "Cost: " << weightSum << "\n";
delete set;
}
// 발견했으나 방문하지 않은 정점 중 가장 가까운 정점 리턴
virtual Edge GetMinVertex(int u, bool* visited, bool* found)
{
int minW = INF;
int minV = 0;
for (int i = 0; i < n; i++)
{
if (i == u) continue; // 자기 자신은 스킵
if (found[i] && !visited[i]) // 발견했는데 방문하지 않은 정점이고
{
if (dist[i] < minW) // 가중치가 가장 작은 것을 찾으면
{
minW = dist[i];
minV = i;
}
}
}
std::cout << "Min: " << u << " " << minV << " " << minW << "\n";
return {u, minV, minW};
}
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation(int v, bool* visited, bool* found) = 0;
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation_Dijkstra(int v, bool* visited, bool* found) = 0;
void Prim(int v)
{
int weightSum = 0;
bool* visited = new bool[n + 1]; // 방문한 정점
bool* found = new bool[n + 1]; // 발견한 정점
std::fill(visited, visited + n + 1, false);
std::fill(found, found + n + 1, false);
std::fill(dist, dist + n + 1, INF); // 거리 배열 초기화
dist[v] = 0; // 시작 정점 거리 설정
visited[v] = true; // 시작 정점 방문 처리
found[v] = true; // 시작 정점 발견 처리
int visitedCnt = 1;
while (visitedCnt < n) // n-1개의 간선을 선택할 때까지
{
Relaxation(v, visited, found);
Edge closestEdge = GetMinVertex(v, visited, found); // v와 인접한 정점 중 가장 가까운 정점으로 연결되는 간선
visited[closestEdge.v] = true; // 방문 처리
visitedCnt++;
weightSum += closestEdge.weight;
std::cout << v << " - " << closestEdge.v << "\n";
v = closestEdge.v;
}
std::cout << "Weight: " << weightSum << "\n";
delete visited;
delete found;
}
void Dijkstra(int v)
{
int weightSum = 0;
bool* visited = new bool[n + 1];
bool* found = new bool[n + 1];
std::fill(visited, visited + n + 1, false);
std::fill(found, found + n +1, false);
std::fill(dist, dist + n + 1, INF); // 거리 배열 초기화
dist[v] = 0;
visited[v] = true;
found[v] = true;
int visitedCnt = 1;
while (visitedCnt < n) // n-1개의 간선을 선택할 때까지
{
Relaxation_Dijkstra(v, visited, found);
Edge closestEdge = GetMinVertex(v, visited, found); // v와 인접한 정점 중 가장 가까운 정점으로 연결되는 간선
visited[closestEdge.v] = true; // 방문 처리
visitedCnt++;
weightSum += closestEdge.weight;
std::cout << v << " - " << closestEdge.v << "\n";
v = closestEdge.v;
}
// 모든 정점까지 이동하는데 필요한 최단 거리 출력
std::cout << "Result Dist: ";
for (int i = 0; i < n; i++)
std::cout << dist[i] << " ";
std::cout << "\n";
delete visited;
delete found;
}
protected:
int n; // 정점의 수
int e; // 간선의 수
std::vector<Edge> edges; // 모든 간선 집합
int* dist; // 거리 배열
};// MatrixWGraph.hpp
#include "Graph.hpp"
class MatrixWGraph : public Graph
{
public:
MatrixWGraph(int vertexCnt)
{
n = vertexCnt; // 정점 개수 설정
e = 0; // 간선 개수 설정
// 이차원 배열 동적 할당
adjMatrix = new int*[n + 1];
for (int i = 0; i <= n; i++)
{
adjMatrix[i] = new int[n + 1];
std::fill(adjMatrix[i], adjMatrix[i] + n + 1, 0); // 0으로 채우기
}
dist = new int[n + 1]; // 거리 배열 할당
}
~MatrixWGraph()
{
for (int i = 0; i <= n; i++)
{
delete adjMatrix[i];
}
delete adjMatrix;
delete dist; // 거리 배열 삭제
}
void PrintAdjMatrix()
{
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
std::cout << adjMatrix[i][j] << " ";
}
std::cout << "\n";
}
}
// 정점 u에 인접한 간선 수 리턴
virtual int Degree(int u) const
{
int edgeCnt = 0;
for (int i = 0; i < n+1; i++)
{
if (adjMatrix[u][i] != 0)
edgeCnt++;
}
return edgeCnt;
}
// 그래프에 간선 (u,v)가 있으면 true 리턴
virtual bool ExistsEdge(int u, int v) const
{
if (adjMatrix[u][v] != 0)
return true;
else
return false;
}
// 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v)
{
adjMatrix[u][v] = 1; // 무방향 그래프
adjMatrix[v][u] = 1;
edges.push_back({u, v, 1}); // 간선 리스트 추가
}
// 가중치가 w인 간선 (u,v)를 그래프에 삽입
virtual void InsertEdge(int u, int v, int w)
{
adjMatrix[u][v] = w; // 무방향 그래프
adjMatrix[v][u] = w;
edges.push_back({u, v, w}); // 간선 리스트 추가
}
// 그래프에서 간선 (u,v) 삭제
virtual void DeleteEdge(int u, int v)
{
adjMatrix[u][v] = 0; // 무방향 그래프
adjMatrix[v][u] = 0;
}
void DFSWrapper(int v)
{
bool* visited = new bool[n + 1];
DFS(v, visited);
delete visited;
}
void DFS(int v, bool* visited)
{
visited[v] = true;
std::cout << v << " ";
for(int i = 0; i <= n; i++)
{
if (adjMatrix[v][i] && !visited[i]) // 인접한 정점 중 방문하지 않은 정점이 있으면
DFS(i, visited);
}
}
void BFS(int v)
{
bool* visited = new bool[n + 1];
std::queue<int> q;
// 시작 정점 큐에 추가
q.push(v);
visited[v] = true;
while (!q.empty())
{
int front = q.front();
q.pop();
std::cout << front << " ";
for (int i = 0; i <= n; i++)
{
if (adjMatrix[front][i] && !visited[i]) // 인접한 정점 중 방문하지 않은 정점이 있다면
{
q.push(i);
visited[i] = true; // 방문 처리
}
}
}
delete visited;
}
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation(int v, bool* visited, bool* found)
{
for (int i = 0; i < n; i++)
{
if (i == v) continue; // 자기 자신이면 스킵
if (adjMatrix[v][i] == 0) continue; // 간선 존재하지 않으면 스킵
if (!visited[i]) // 방문하지 않은 정점이고
{
if (adjMatrix[v][i] < dist[i]) // 더 짧은 거리를 찾았으면
dist[i] = adjMatrix[v][i]; // 거리 업데이트
found[i] = true; // 발견 여부 업데이트
}
}
}
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation_Dijkstra(int v, bool* visited, bool* found)
{
for (int i = 0; i < n; i++)
{
if (i == v) continue; // 자기 자신이면 스킵
if (adjMatrix[v][i] == 0) continue; // 간선 존재하지 않으면 스킵
if (!visited[i]) // 방문하지 않은 정점이고
{
if (dist[v] + adjMatrix[v][i] < dist[i]) // 더 짧은 거리를 찾았으면
dist[i] = dist[v] + adjMatrix[v][i]; // 거리 업데이트
found[i] = true; // 발견 여부 업데이트
}
}
// 모든 정점까지 이동하는데 필요한 최단 거리 출력
std::cout << "Dist: ";
for (int i = 0; i < n; i++)
std::cout << dist[i] << " ";
std::cout << "\n";
}
private:
int** adjMatrix; // 인접 행렬
};// LinkedWGraph.hpp
#include "Graph.hpp"
#include "../../Chapter4/4.10/DoublyLinkedList.hpp"
class LinkedWGraph : public Graph
{
public:
LinkedWGraph(int vertexCnt)
{
n = vertexCnt; // 정점 개수 설정
e = 0;
adjList = new DoublyLinkedList<int>[n]; // 인접 리스트 할당
for (int i = 0; i <= n; i++)
{
adjList[i].head = new BidirectionalNode<int>(i);
}
dist = new int[n + 1]; // 거리 배열 할당
}
~LinkedWGraph()
{
delete adjList; // 인접 리스트 삭제
}
void PrintAdjList()
{
for (int i = 0; i <= n; i++)
{
std::cout << i << ": ";
BidirectionalNode<int>* curr = adjList[i].head->right;
while (curr)
{
std::cout << curr->data << " -> ";
curr = curr->right;
}
std::cout << "nullptr\n";
}
}
// 정점 u에 인접한 간선 수 리턴
virtual int Degree(int u) const
{
int edgeCnt = 0;
BidirectionalNode<int>* curr = adjList[u].head->right; // 뒤에 연결된 인접한 정점부터 시작
while (curr)
{
edgeCnt++;
curr = curr->right;
}
return edgeCnt;
}
// 그래프에 간선 (u,v)가 있으면 true 리턴
virtual bool ExistsEdge(int u, int v) const
{
BidirectionalNode<int>* curr = adjList[u].head;
while (curr)
{
if (curr->data == v) // 연결된 인접 정점 중 v가 있으면
return true;
curr = curr->right;
}
return false; // 없는 경우
}
// 간선 (u,v)를 그래프에 삽입
// 양방향 그래프이므로 양쪽에 삽입
virtual void InsertEdge(int u, int v)
{
BidirectionalNode<int>* uVert = new BidirectionalNode<int>(u); // 새로운 정점 노드
BidirectionalNode<int>* vVert = new BidirectionalNode<int>(v);
adjList[u].Insert(vVert, adjList[u].GetLastNode()); // 리스트 맨 뒤에 추가
adjList[v].Insert(uVert, adjList[v].GetLastNode());
edges.push_back({u, v, 1});
}
// 가중치가 w인 간선 (u,v)를 그래프에 삽입
// 양방향 그래프이므로 양쪽에 삽입
virtual void InsertEdge(int u, int v, int w)
{
BidirectionalNode<int>* uVert = new BidirectionalNode<int>(u, w); // 새로운 정점 노드
BidirectionalNode<int>* vVert = new BidirectionalNode<int>(v, w);
adjList[u].Insert(vVert, adjList[u].GetLastNode()); // 리스트 맨 뒤에 추가
adjList[v].Insert(uVert, adjList[v].GetLastNode());
edges.push_back({u, v, w});
}
// 그래프에서 간선 (u,v) 삭제
virtual void DeleteEdge(int u, int v)
{
BidirectionalNode<int>* vNode = adjList[u].Find(v);
adjList[u].Delete(vNode);
}
// DFS
void DFSWrapper(int v)
{
bool* visited = new bool[n + 1];
DFS(v, visited);
delete visited;
}
void DFS(int v, bool* visited)
{
visited[v] = true; // 방문 처리
std::cout << v << " ";
BidirectionalNode<int>* curr = adjList[v].head->right; // 인접한 정점의 노드부터 시작
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았으면
DFS(curr->data, visited);
curr = curr->right;
}
}
// BFS
void BFS(int v)
{
bool* visited = new bool[n + 1];
std::queue<int> q;
// 시작 정점 큐에 추가
q.push(v);
visited[v] = true;
while (!q.empty())
{
int front = q.front();
q.pop();
std::cout << front << " ";
BidirectionalNode<int>* curr = adjList[front].head->right; // 인접한 정점의 노드부터 시작
while (curr)
{
if (!visited[curr->data]) // 인접한 정점 중 방문 안 한 노드가 있으면
{
q.push(curr->data); // 큐 추가
visited[curr->data] = true; // 방문 처리
}
curr = curr->right;
}
}
delete visited;
}
virtual void Relaxation(int v, bool* visited, bool* found)
{
BidirectionalNode<int>* curr = adjList[v].head->right;
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았고
{
if (curr->weight < dist[curr->data]) // 기존에 알고 있던 거리보다 더 짧은 경로가 있으면
dist[curr->data] = curr->weight; // 거리 업데이트
found[curr->data] = true; // 발견 여부 저장
}
curr = curr->right;
}
}
// 인접한 정점 중 거리 업데이트 할 정점이 있는 지 확인
virtual void Relaxation_Dijkstra(int v, bool* visited, bool* found)
{
BidirectionalNode<int>* vVert = adjList[v].head;
BidirectionalNode<int>* curr = vVert->right;
while (curr)
{
if (!visited[curr->data]) // 방문하지 않았고
{
if (dist[vVert->data] + curr->weight < dist[curr->data]) // 새로 찾은 누적 경로가 dist에 담긴 거리보다 짧으면
dist[curr->data] = dist[vVert->data] + curr->weight; // 거리 업데이트
found[curr->data] = true; // 발견 여부 저장
}
curr = curr->right;
}
// 모든 정점까지 이동하는데 필요한 최단 거리 출력
std::cout << "Dist: ";
for (int i = 0; i < n; i++)
std::cout << dist[i] << " ";
std::cout << "\n";
}
private:
DoublyLinkedList<int>* adjList;
};728x90
'Programming > Algorithm & Data Structure' 카테고리의 다른 글
| [Data Structure] AVL 트리 (0) | 2025.01.18 |
|---|---|
| [Data Structure] 신장 트리, 최소 비용 신장 트리와 Kruskal, Prim 알고리즘 (0) | 2025.01.13 |
| [Data Structure] 그래프와 기본 연산 (BFS, DFS) (0) | 2025.01.13 |
| [Data Structure] 이진 탐색 트리 (0) | 2025.01.13 |
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2025.01.13 |
