728x90
이진 트리의 문제점
- 이진 트리의 경우 균형이 잡혀있다면 삽입, 삭제, 검색을 할 때 O(logn)의 시간 복잡도를 기대할 수 있지만, 한 쪽으로 편향되어 있다면 선형 자료구조처럼 작동해 O(n)의 시간 복잡도를 가지게 된다.
- 그러므로 이진 트리의 균형을 맞추는 것은 중요하다.


AVL 트리
- AVL 트리는 스스로 균형을 잡는 자가 균형 이진 탐색 트리이다.
- 어떤 노드의 두 자식 서브트리의 높이의 차이가 최대 1만큼만 차이난다.
- 어떤 시점에서 높이 차이가 1보다 커지면 균형이 무너졌다고 판단해 회전을 통해 스스로 균형을 잡는다.
- 검색, 삽입, 삭제는 평균과 최악의 경우 모두 O(log n)의 시간 복잡도가 걸린다.
Balance Factor
- AVL 트리에서 균형의 무너짐을 판단하는 기준이다.
Balance Factor 계산식
어떤 노드 k에 대해
BF(k) = k의 왼쪽 서브트리 높이 - k의 오른쪽 서브트리 높이
- AVL 트리는 모든 노드의 BF가 -1, 0, 1 이여야 하고, 그 외의 값을 가질 경우 균형이 무너진 것으로 판단한다.

회전 종류
- AVL 트리의 회전 종류는 두 가지가 있다.
- 아래 회전 예제에서는 z를 기준으로 회전한다.
우회전(Right Rotation)
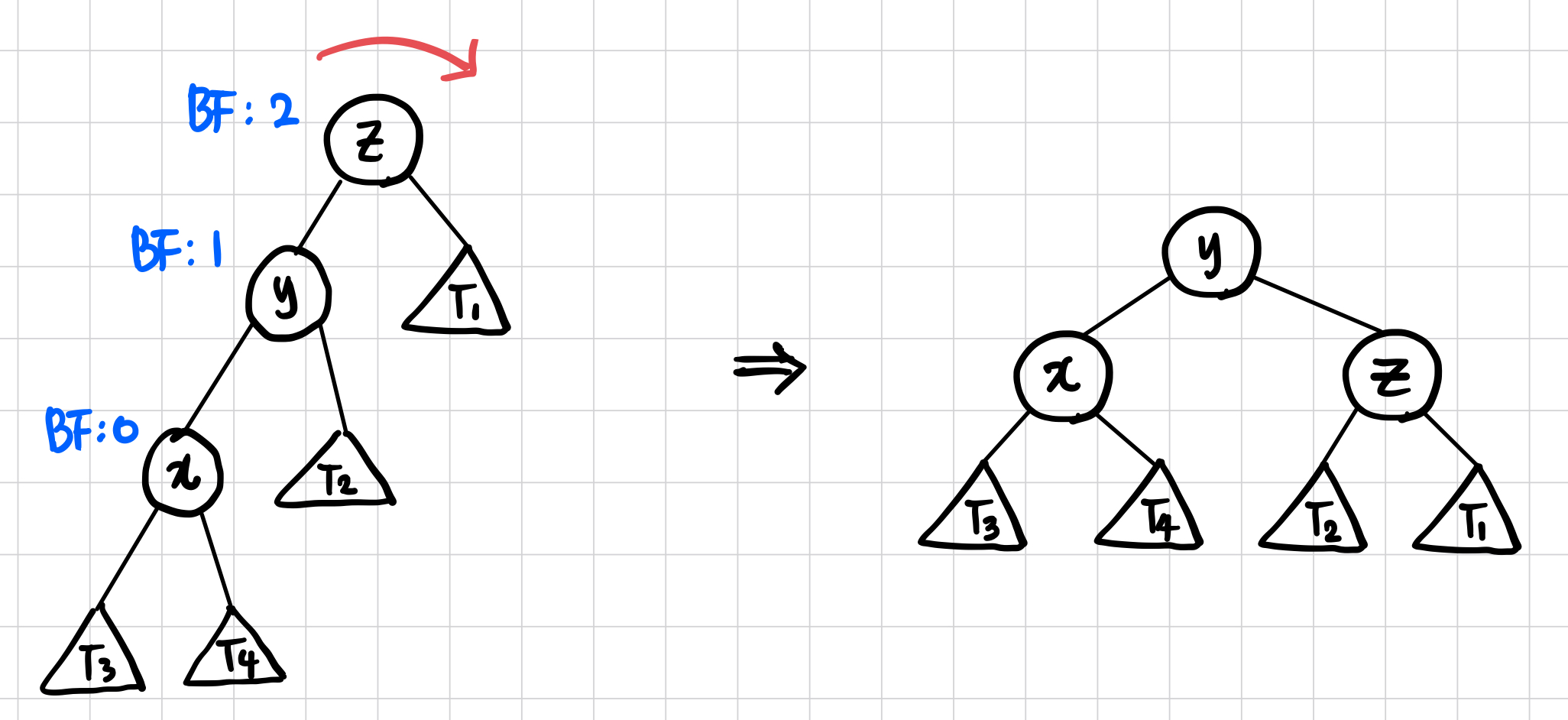
- y 노드의 오른쪽 자식 노드를 z 노드로 바꾼다.
- z 노드의 왼쪽 자식을 y 노드의 오른쪽 서브트리로 변경한다.
좌회전(Left Rotation)
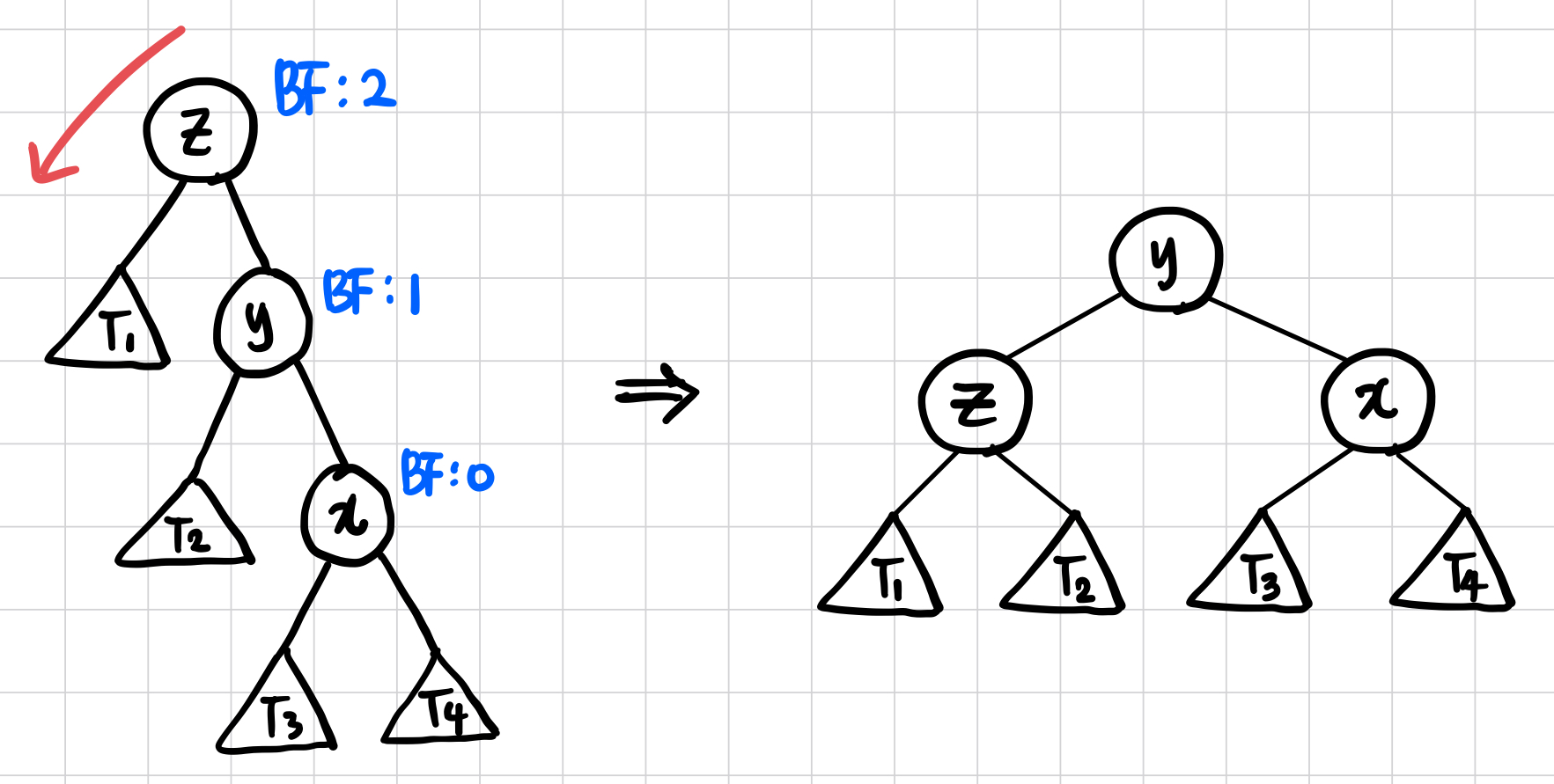
- y 노드의 왼쪽 자식을 z 노드로 바꾼다.
- z 노드의 오른쪽 자식을 y 노드의 왼쪽 서브트리로 변경한다.
균형이 무너진 케이스 (LL, LR, RL, RR)
- AVL 트리에서는 4개의 균형이 무너진 케이스가 있다.
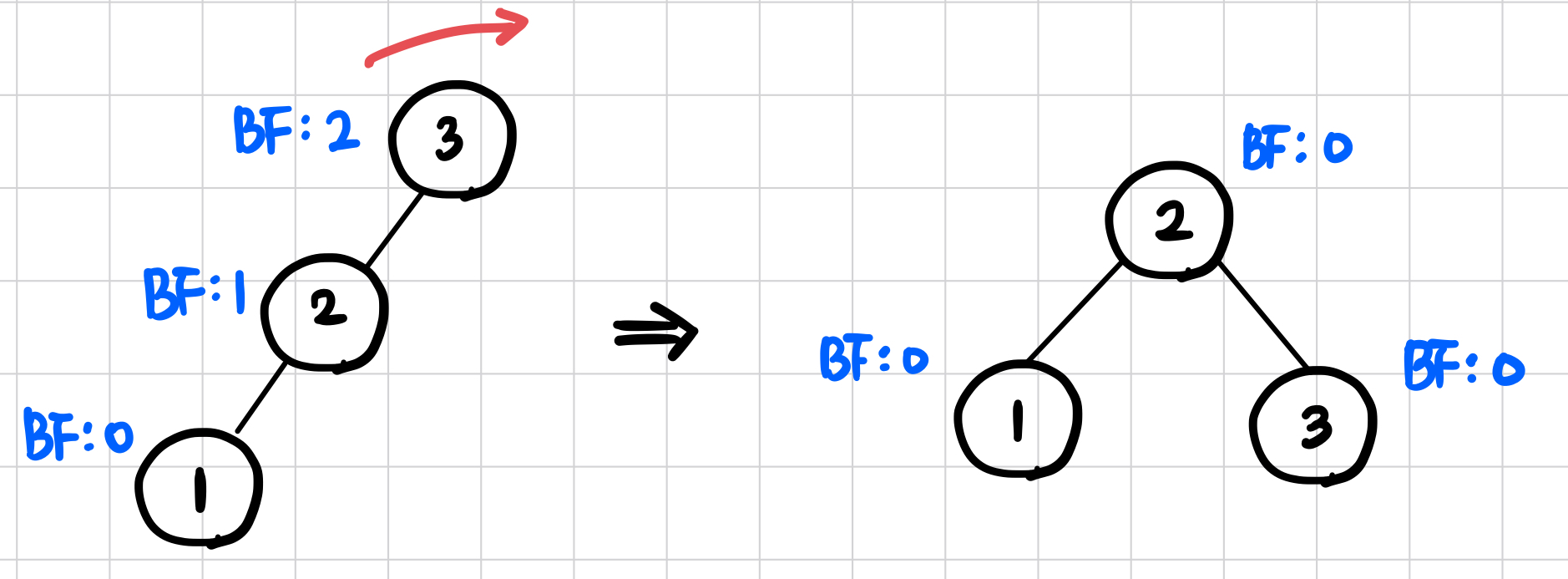
LL(Left Left) Case
- 밸런스가 -1 ~ 1을 벗어난 노드를 기준으로 왼쪽으로 연달아 2개의 노드가 존재하는 경우
- 해당 노드를 기준으로 우회전 해 균형을 맞춘다.
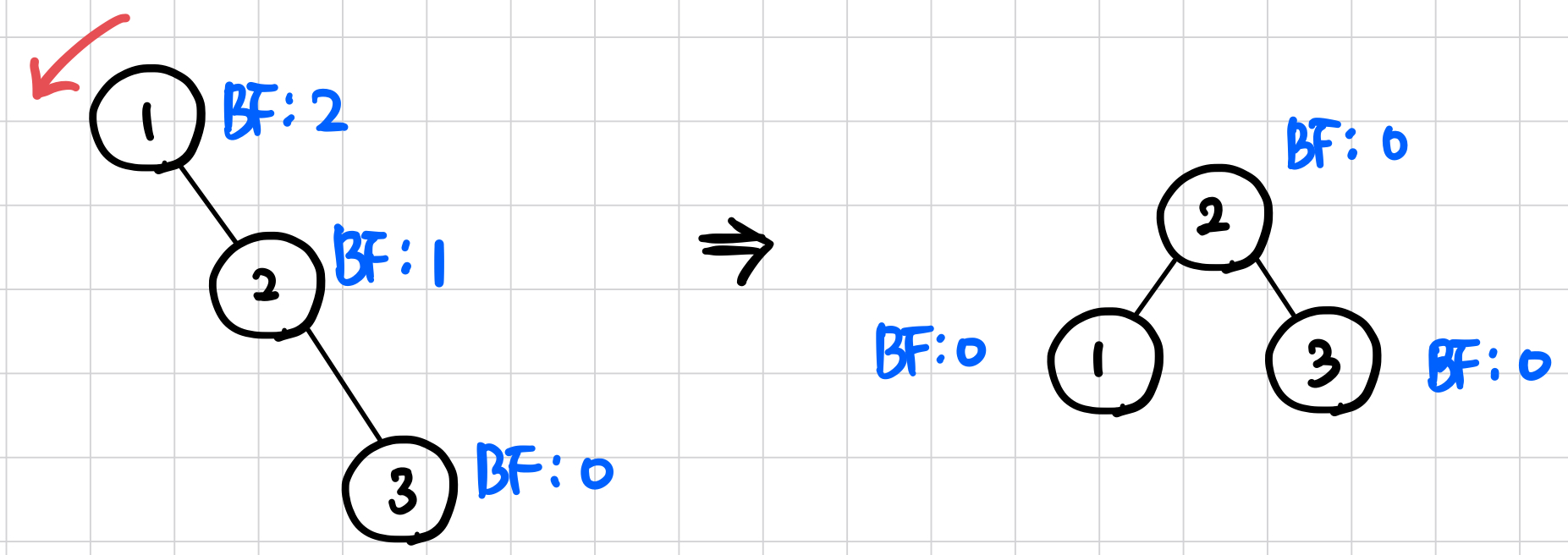
RR(Right Right) Case
- 밸런스가 -1 ~ 1을 벗어난 노드를 기준으로 오른쪽으로 연달아 2개의 노드가 존재하는 경우
- 해당 노드를 기준으로 좌회전 해 균형을 맞춘다.
LR(Left Right) Case
- 밸런스가 -1 ~ 1을 벗어난 노드를 기준으로 왼쪽→오른쪽 노드가 존재하는 경우
- 해당 노드에 대해
- 왼쪽 자식 노드를 기준으로 좌회전
- 해당 노드를 기준으로 우회전
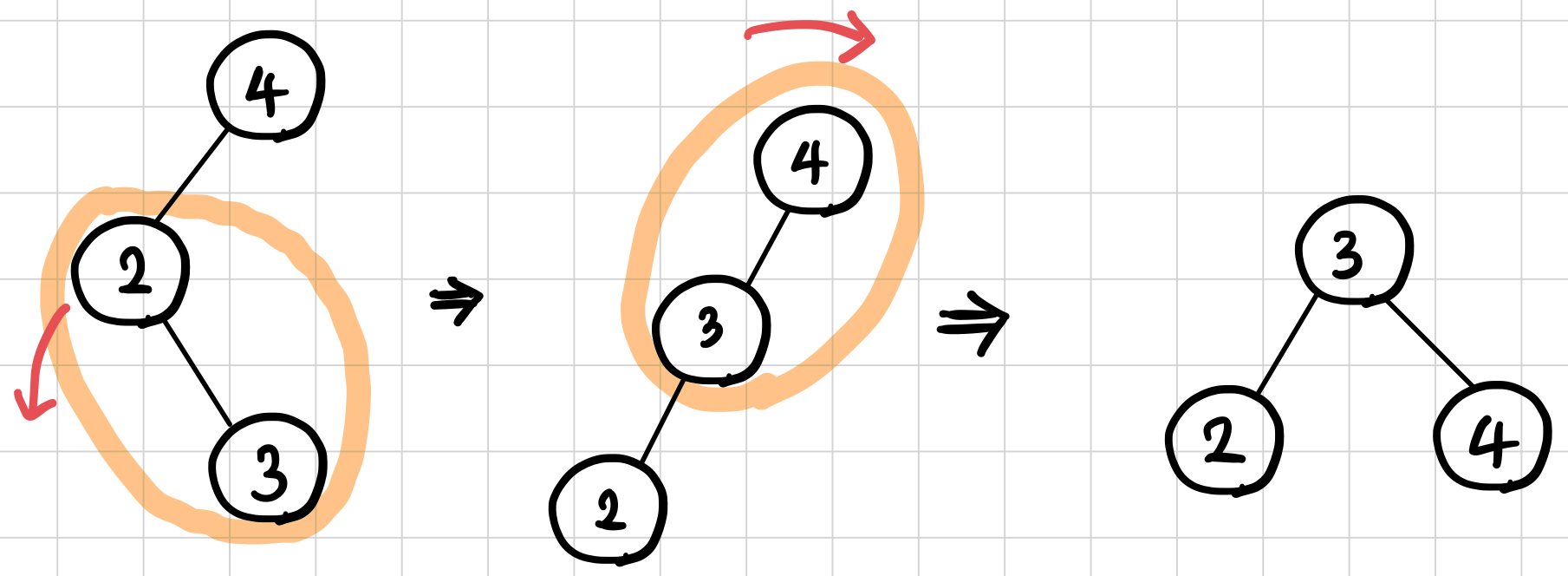
RL(Right Left) Case
- 밸런스가 -1 ~ 1을 벗어난 노드를 기준으로 오른쪽→왼쪽 노드가 존재하는 경우
- 해당 노드에 대해
- 오른쪽 자식 노드를 기준으로 우회전
- 해당 노드를 기준으로 좌회전

참고 자료
AVL 트리 시각화: https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
728x90
'Programming > Algorithm & Data Structure' 카테고리의 다른 글
| [Algorithm] 최단 경로 - Dijkstra 알고리즘 (0) | 2025.01.13 |
|---|---|
| [Data Structure] 신장 트리, 최소 비용 신장 트리와 Kruskal, Prim 알고리즘 (0) | 2025.01.13 |
| [Data Structure] 그래프와 기본 연산 (BFS, DFS) (0) | 2025.01.13 |
| [Data Structure] 이진 탐색 트리 (0) | 2025.01.13 |
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2025.01.13 |
